
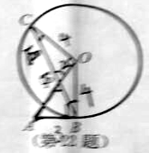
【题目】如图,![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 为
为![]() 的弦,
的弦,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ;
;
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)详见解析;(2)BP=![]() .
.
【解析】
试题分析:(1)根据已知条件易得∠ABP+∠OBC=90°,∠C+∠CPO=90°,因为∠APB=∠CPO, 即可得∠C+∠APB=90°,再由∠C=∠OBC,即可得∠ABP=∠APB,所以AP=AB;(2)过点A作AD![]() BP,垂足为D,所以∠ADP=90°,PD=
BP,垂足为D,所以∠ADP=90°,PD=![]() BP,由勾股定理求得OA的长,再由勾股定理求得CP的长,由∠ADP=∠CPO,∠ADP=∠COP,证得△ADP∽△COP,根据相似三角形的性质求得PD的长,即可得BP的长.
BP,由勾股定理求得OA的长,再由勾股定理求得CP的长,由∠ADP=∠CPO,∠ADP=∠COP,证得△ADP∽△COP,根据相似三角形的性质求得PD的长,即可得BP的长.
试题解析:(1)因为![]() 与
与![]() 相切于点
相切于点![]() ,所以
,所以![]() ,∠ABP+∠OBC=90°,
,∠ABP+∠OBC=90°,
因为![]() ,所以∠C+∠CPO=90°,
,所以∠C+∠CPO=90°,
因为∠APB=∠CPO,所以∠C+∠APB=90°,
因为OC=OB,所以∠C=∠OBC,
所以∠ABP=∠APB,
因此AP=AB.
(2) 过点A作AD![]() BP,垂足为D,所以∠ADP=90°,PD=
BP,垂足为D,所以∠ADP=90°,PD=![]() BP
BP
因为∠ABO=90°,![]() ,
,![]() ,所以
,所以![]() ,故OA=5
,故OA=5
因为AP=AB=3,所以OP=OA-AP=2
因为∠COP=90°,所以![]() ,
,
因为∠ADP=∠CPO,∠ADP=∠COP,所以△ADP∽△COP.
所以![]() ,即PD=
,即PD=![]() ,所以BP=
,所以BP=![]() .
.



科目:初中数学 来源: 题型:
【题目】一只盒子中有红球m个,白球6个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得是白球的概率与不是白球的概率相同,那么m与n的关系是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生最喜欢的球类情况,随机抽取了八年级部分学生进行问卷调查,调查分为最喜欢篮球、乒乓球、足球、排球共四种情况,每名同学选且只选一项.现将调查结果绘制成如下所示的两幅统计图.

请结合这两幅统计图,解决下列问题:
(1)在这次问卷调查中,一共抽取了 名学生;
(2)请补全条形统计图;
(3)若该校八年级共有![]() 名学生,请你估计其中最喜欢排球的学生人数.
名学生,请你估计其中最喜欢排球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
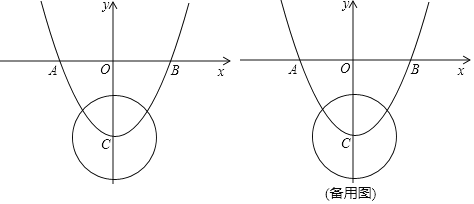
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点与
两点与![]() 轴交于点
轴交于点![]() ,⊙
,⊙![]() 的半径为
的半径为![]() 为⊙
为⊙![]() 上一动点.
上一动点.
(1)点![]() 的坐标分别为
的坐标分别为![]() ( ),
( ),![]() ( );
( );
(2)是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)连接![]() ,若
,若![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的最大值= .
的最大值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线![]() 经过A、C两点,与x轴的另一交点为点B.
经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为![]() ,△BCE的面积为
,△BCE的面积为![]() ,求
,求![]() 的最大值;
的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点
的顶点![]() 是坐标原点,点
是坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 分别为四边形
分别为四边形![]() 边上的动点,动点
边上的动点,动点![]() 从点
从点![]() 开始,以每秒1个单位长度的速度沿
开始,以每秒1个单位长度的速度沿![]() 路线向中点
路线向中点![]() 匀速运动,动点
匀速运动,动点![]() 从
从![]() 点开始,以每秒两个单位长度的速度沿
点开始,以每秒两个单位长度的速度沿![]() 路线向终点
路线向终点![]() 匀速运动,点
匀速运动,点![]() 同时从
同时从![]() 点出发,当其中一点到达终点后,另一点也随之停止运动。设动点运动的时间
点出发,当其中一点到达终点后,另一点也随之停止运动。设动点运动的时间![]() 秒(
秒(![]() ),
),![]() 的面积为
的面积为![]() .
.
(1)填空:![]() 的长是 ,
的长是 ,![]() 的长是 ;
的长是 ;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)当![]() 时,设点
时,设点![]() 的纵坐标为
的纵坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)若![]() ,请直接写出此时
,请直接写出此时![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com