
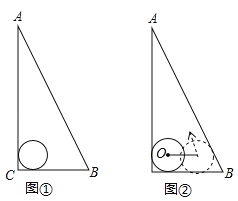
【题目】如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.
【答案】(1)作图见解析;(2)![]() .
.
【解析】
试题分析:(1)作∠ACB的平分线得出圆的一条弦,再作此弦的中垂线可得圆心O,作射线CO即可;
(2)添加如图所示辅助线,圆心O的运动路径长为![]() ,先求出△ABC的三边长度,得出其周长,证四边形OEDO1、四边形O1O2HG、四边形OO2IF均为矩形、四边形OECF为正方形,得出∠OO1O2=60°=∠ABC、∠O1OO2=90°,从而知△OO1O2∽△CBA,利用相似三角形的性质即可得出答案.
,先求出△ABC的三边长度,得出其周长,证四边形OEDO1、四边形O1O2HG、四边形OO2IF均为矩形、四边形OECF为正方形,得出∠OO1O2=60°=∠ABC、∠O1OO2=90°,从而知△OO1O2∽△CBA,利用相似三角形的性质即可得出答案.
试题解析:(1)如图①所示,射线OC即为所求;
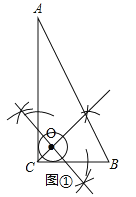
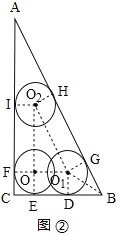
(2)如图2,圆心O的运动路径长为![]() ,过点O1作O1D⊥BC、O1F⊥AC、O1G⊥AB,垂足分别为点D、F、G,过点O作OE⊥BC,垂足为点E,连接O2B,过点O2作O2H⊥AB,O2I⊥AC,垂足分别为点H、I,在Rt△ABC中,∠ACB=90°、∠A=30°,∴AC=
,过点O1作O1D⊥BC、O1F⊥AC、O1G⊥AB,垂足分别为点D、F、G,过点O作OE⊥BC,垂足为点E,连接O2B,过点O2作O2H⊥AB,O2I⊥AC,垂足分别为点H、I,在Rt△ABC中,∠ACB=90°、∠A=30°,∴AC=![]() =
=![]() =
=![]() ,AB=2BC=18,∠ABC=60°,∴C△ABC=9+
,AB=2BC=18,∠ABC=60°,∴C△ABC=9+![]() +18=27+
+18=27+![]() ,∵O1D⊥BC、O1G⊥AB,∴D、G为切点,∴BD=BG,在Rt△O1BD和Rt△O1BG中,∵BD=BG,O1B=O1B,∴△O1BD≌△O1BG(HL),∴∠O1BG=∠O1BD=30°,在Rt△O1BD中,∠O1DB=90°,∠O1BD=30°,∴BD=
,∵O1D⊥BC、O1G⊥AB,∴D、G为切点,∴BD=BG,在Rt△O1BD和Rt△O1BG中,∵BD=BG,O1B=O1B,∴△O1BD≌△O1BG(HL),∴∠O1BG=∠O1BD=30°,在Rt△O1BD中,∠O1DB=90°,∠O1BD=30°,∴BD=![]() =
=![]() =
=![]() ,∴OO1=9﹣2﹣
,∴OO1=9﹣2﹣![]() =7﹣
=7﹣![]() ,∵O1D=OE=2,O1D⊥BC,OE⊥BC,∴O1D∥OE,且O1D=OE,∴四边形OEDO1为平行四边形,∵∠OED=90°,∴四边形OEDO1为矩形,同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,又OE=OF,∴四边形OECF为正方形,∵∠O1GH=∠CDO1=90°,∠ABC=60°,∴∠GO1D=120°,又∵∠FO1D=∠O2O1G=90°,∴∠OO1O2=360°﹣90°﹣90°=60°=∠ABC,同理,∠O1OO2=90°,∴△OO1O2∽△CBA,∴
,∵O1D=OE=2,O1D⊥BC,OE⊥BC,∴O1D∥OE,且O1D=OE,∴四边形OEDO1为平行四边形,∵∠OED=90°,∴四边形OEDO1为矩形,同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,又OE=OF,∴四边形OECF为正方形,∵∠O1GH=∠CDO1=90°,∠ABC=60°,∴∠GO1D=120°,又∵∠FO1D=∠O2O1G=90°,∴∠OO1O2=360°﹣90°﹣90°=60°=∠ABC,同理,∠O1OO2=90°,∴△OO1O2∽△CBA,∴![]() ,即
,即![]() ,∴
,∴![]() =
=![]() ,即圆心O运动的路径长为
,即圆心O运动的路径长为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系 ![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;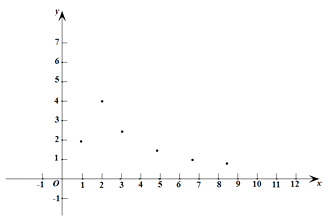
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为;
②该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).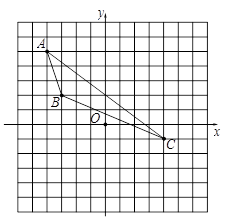
(1)作出△ABC关于x轴对称的图形△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)若AC=10,求△ABC的AC边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论错误的是( )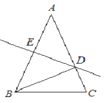
A.BD平分∠ABC
B.
△BCD的周长等于AB+BC
C.AD=BD=BC
D.点D是线段AC的中点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com