
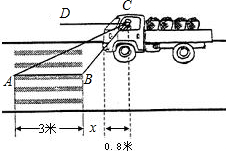
 ��ͼ��һλ��ʻԱ����ǰ���������������˺ᴩ��·����ȡ����ɲ������������12�����ͣ�£�
��ͼ��һλ��ʻԱ����ǰ���������������˺ᴩ��·����ȡ����ɲ������������12�����ͣ�£����� ��1����s=12���빫ʽ���鹫ʽ��s=$\frac{v^2}{300}$�������Ӧ���ٶȣ�Ȼ����80km/h�Ƚϼ��ɵõ��𰸣�
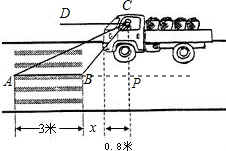
��2����ͼ����CP��AB����AB�ӳ����ڵ�P��ͨ����ֱ�ǡ�BCP�͡�ACP�õ��߶�BP��AP�ij��ȣ���AB=AP-BP=2BP��
��� �⣺ ��1���ɾ��鹫ʽs=$\frac{v^2}{300}$����
��1���ɾ��鹫ʽs=$\frac{v^2}{300}$����
��s=12ʱ��v2=3600����v=60��80��
���ԣ�û�г��٣�
��2����ͼ����CP��AB����AB�ӳ����ڵ�P��
�ߡ�CBP=60�㣬
��CP=BP•tan60��=$\sqrt{3}BP$
�ߡ�CAP=30�㣬
��AP=$\frac{CP}{tan30��}$=$\sqrt{3}CP$=3BP
��AB=AP-BP=2BP=3��
��BP=1.5��
��x=0.7��
���� ���⿼���˽�ֱ�������ε�Ӧ�ã���Ҫ�����С����и�����㣬�ؼ���ʵ������ת��Ϊ��ѧ������Լ��㣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
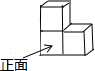 ��ͼ��������С�������ɵļ����壬��������������ͼ�ǣ�������
��ͼ��������С�������ɵļ����壬��������������ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
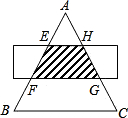 ��ͼ����ABC�DZ߳�Ϊ12cm�ĵȱ������Σ���һƽ����BC�ľ������أ�AB���س����ȷ֣���ͼ����Ӱ���ֵ����Ϊ��������
��ͼ����ABC�DZ߳�Ϊ12cm�ĵȱ������Σ���һƽ����BC�ľ������أ�AB���س����ȷ֣���ͼ����Ӱ���ֵ����Ϊ��������| A�� | 16cm2 | B�� | $8\sqrt{3}$cm2 | C�� | $16\sqrt{3}$cm2 | D�� | $12\sqrt{3}$cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
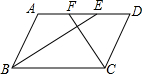 ��ͼ��ƽ���ı���ABCD�У�AB=2cm��BC=3cm����ABC����BCD��ƽ���߷ֱ�AD�ڵ�F��E����EF�ij�Ϊ1cm��
��ͼ��ƽ���ı���ABCD�У�AB=2cm��BC=3cm����ABC����BCD��ƽ���߷ֱ�AD�ڵ�F��E����EF�ij�Ϊ1cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | 0 | 1 | 2 |
| 2x2-1 | -1 | 1 | 7 |
| x | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| 2x2-1 | -0.5 | -0.28 | -0.2 | 0.28 | 0.62 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com