
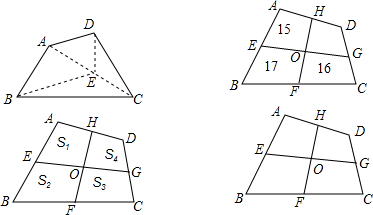
分析 由阅读材料可知:三角形的中线将三角形分成面积相等的两部分.条件中出现了线段的中点,问题中涉及到面积,由此联想到“三角形的中线将三角形分成面积相等的两部分”,故而连接OA、OB、OC、OD,即可得到S△AOE=S△BOE,S△BOF=S△COF,S△COG=S△DOG,S△DOH=S△AOH.
(1)由题可得S△AOE+S△AOH=15①,S△BOE+S△BOF=17②,S△COF+S△COG=16③,只需将①+③-②,就可解决问题;
(2)由题可得S△AOE+S△AOH=S1,S△BOE+S△BOF=S2,S△COF+S△COG=S3,S△DOG+S△DOH=S4,而S1+S3=S△AOE+S△AOH+S△COF+S△COG,S2+S4=S△BOE+S△BOF+S△DOG+S△DOH,即可得到S1+S3=S2+S4.
解答 解:(1)连接OA、OB、OC、OD,如图1,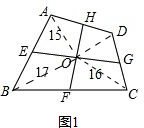
∵点E,F,G,H,分别是AB,BC,CD,DE的中点,
∴S△AOE=S△BOE,S△BOF=S△COF,S△COG=S△DOG,S△DOH=S△AOH,
∵S△AOE+S△AOH=15①,S△BOE+S△BOF=17②,S△COF+S△COG=16③,
∴由①+③-②得S△AOH+S△COG=15+16-17=14,
∴S四边形DGOH=S△DOH+S△DOG=S△AOH+S△COG=14.
故答案为14;
(2)连接OA、OB、OC、OD,如图2,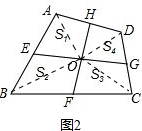
∵点E,F,G,H,分别是AB,BC,CD,DE的中点,
∴S△AOE=S△BOE,S△BOF=S△COF,S△COG=S△DOG,S△DOH=S△AOH.
∵S△AOE+S△AOH=S1,S△BOE+S△BOF=S2,S△COF+S△COG=S3,S△DOG+S△DOH=S4,
∴S1+S3=S△AOE+S△AOH+S△COF+S△COG,S2+S4=S△BOE+S△BOF+S△DOG+S△DOH,
∴S1+S3=S2+S4.
故答案为S1+S3=S2+S4.
点评 本题主要考查了“三角形的中线将三角形分成面积相等的两部分”的应用,由线段的中点联想到三角形的中线将三角形分成面积相等的两部分,是解决本题的关键.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:解答题
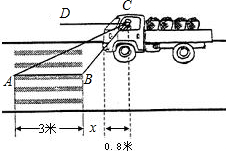 如图,一位驾驶员看到前方斑马线上有行人横穿马路,采取紧急刹车,汽车滑行12米距离后停下,
如图,一位驾驶员看到前方斑马线上有行人横穿马路,采取紧急刹车,汽车滑行12米距离后停下,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
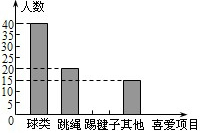 某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.
某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com