
【题目】如图,在ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.

【答案】(1)详见解析;(2)四边形ABEF是菱形,理由详见解析.
【解析】
试题分析:(1)由角平分线的作法容易得出结果,在AD上截取AF=AB,连接EF;画出图形即可;(2)由平行四边形的性质和角平分线得出∠BAE=∠AEB,证出BE=AB,由(1)得:AF=AB,得出BE=AF,即可得出结论.
试题解析:解:(1)如图所示:
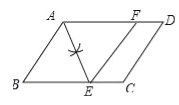
(2)四边形ABEF是菱形;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
由(1)得:AF=AB,
∴BE=AF,
又∵BE∥AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴四边形ABEF是菱形.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】已知线段AB=12,CD=6,线段CD在直线AB上运动(A在B的左侧,C在D的左侧).
(1)当D点与B点重合时,AC=_________;
(2)点P是线段AB延长线上任意一点,在(1)的条件下,求PA+PB–2PC的值;
(3)M、N分别是AC、BD的中点,当BC=4时,求MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师到市教育局大楼办事,他从一楼出发,要去不同楼层办理具体事务,如果约定乘电梯向上一楼记作+1,向下一楼记作-1,那么李老师办事过程中电梯上下楼层依次记录如下:+6,-3,+9,-5,-7.(单位:层)
(1)请说明李老师是否在十三楼办理过事务?
(2)请说明李老师最后是否回到出发点一楼?
(3)该大楼每层高3m,电梯每向上或向下1m大约需要耗电0.01度,请你算算,他办事中电梯需要耗电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广东省梅州市第24题)(为方便答题,可在答题卡上画出你认为必要的图形)
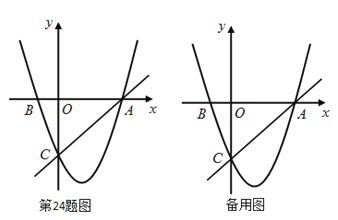
如图,在平面直角坐标系中,已知抛物线![]() 过A,B,C三点,点A的坐标是
过A,B,C三点,点A的坐标是![]() ,点C的坐标是
,点C的坐标是![]() ,动点P在抛物线上.
,动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣5(x+2)2﹣6的对称轴和顶点分别是( )
A. x=2和(2,﹣6) B. x=2和(﹣2,﹣6)
C. x=﹣2和(﹣2,﹣6) D. x=﹣2和(2,﹣6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com