
【题目】在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB. 
(1)当OC∥AB时,∠BOC的度数为;
(2)连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值;
(3)连接AD,当OC∥AD时,①求出点C的坐标;②直线BC是否为⊙O的切线?请作出判断,并说明理由.
【答案】
(1)45°或135°
(2)解:∵△OAB为等腰直角三角形,
∴AB= ![]() OA=6
OA=6 ![]() ,
,
∴当点C到AB的距离最大时,△ABC的面积最大,
过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,如图,

此时C点到AB的距离的最大值为CE的长,
∴OE= ![]() AB=3
AB=3 ![]() ,
,
∴CE=OC+OE=3+3 ![]() ,
,
△ABC的面积= ![]() CEAB=
CEAB= ![]() ×(3+3
×(3+3 ![]() )×6
)×6 ![]() =9
=9 ![]() +18.
+18.
∴当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,
△ABC的面积最大,最大值为9 ![]() +18
+18
(3)解:①如图,过C点作CF⊥x轴于F,

∵OC∥AD,
∴∠COF=∠DAO,
又∵∠ADO=∠CFO=90°
∴Rt△OCF∽Rt△AOD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得CF=
,解得CF= ![]() ,
,
在Rt△OCF中,OF= ![]() =
= ![]() ,
,
∴C点坐标为(﹣ ![]() ,
, ![]() );
);
故所求点C的坐标为(﹣ ![]() ,
, ![]() ),
),
当C点在第一象限时,同理可得C点的坐标为( ![]() ,
, ![]() ),
),
综上可得,点C的坐标为(﹣ ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
②当C点坐标为(﹣ ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )时,直线BC是⊙O的切线.理由如下:
)时,直线BC是⊙O的切线.理由如下:
在Rt△OCF中,OC=3,CF= ![]() ,
,
∴∠COF=30°,
∴∠OAD=30°,
∴∠BOC=60°,∠AOD=60°,
∵在△BOC和△AOD中
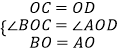 ,
,
∴△BOC≌△AOD(SAS),
∴∠BCO=∠ADO=90°,
∴OC⊥BC,
∴直线BC为⊙O的切线;
当C点坐标为(﹣ ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )时,显然直线BC与⊙O相切.
)时,显然直线BC与⊙O相切.
综上可得:C点坐标为( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() )时,显然直线BC与⊙O相切.
)时,显然直线BC与⊙O相切.

【解析】解:(1)∵点A(6,0),点B(0,6), ∴OA=OB=6,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴当C点在y轴左侧时,∠BOC=∠OBA=45°;
当C点在y轴右侧时,∠BOC=90°+∠OBA=135°;


科目:初中数学 来源: 题型:
【题目】如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是14 ![]() ,则排球的直径是( )
,则排球的直径是( ) 
A.7cm
B.14cm
C.21cm
D.21 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小明按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则下列说法正确的是( )
A.小明打开的一定是楼梯灯;
B.小明打开的可能是卧室灯;
C.小明打开的不可能是客厅灯;
D.小明打开走廊灯的概率是 ![]()
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策,各地政府高度重视、积极响应,中国掀起了大众创业万众创新的新浪潮.某创新公司生产营销A、B两种新产品,根据市场调研,发现如下信息: 信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系y=ax2+bx,当x=1时,y=7;当x=2时,y=12.
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系y=2x.
根据以上信息,解答下列问题:
(1)求a,b的值;
(2)该公司准备生产营销A、B两种产品共10吨,请设计一个生产方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?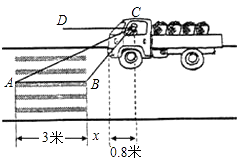
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com