
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНЃx2ЃЋbxЃЋcгывЛжБЯпЯрНЛгкA(Ѓ1ЃЌ0)ЃЌC(2ЃЌ3)СНЕуЃЌгыyжсНЛгкЕуNЃЌЦфЖЅЕуЮЊD.
(1)ЧѓХзЮяЯпМАжБЯпACЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ЩшЕуM(3ЃЌm)ЃЌЧѓЪЙMNЃЋMDЕФжЕзюаЁЪБmЕФжЕЃЛ
(3)ШєХзЮяЯпЕФЖдГЦжсгыжБЯпACЯрНЛгкЕуBЃЌEЮЊжБЯпACЩЯЕФШЮвтвЛЕуЃЌЙ§ЕуEзїEFЁЮBDНЛХзЮяЯпгкЕуFЃЌвдBЃЌDЃЌEЃЌFЮЊЖЅЕуЕФЫФБпаЮФмЗёЮЊЦНааЫФБпаЮЃПШєФмЃЌЧѓЕуEЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
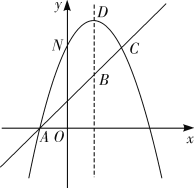
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊyЃНЃx2ЃЋ2xЃЋ3ЃЛжБЯпACЕФНтЮіЪНЮЊyЃНxЃЋ1ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉEЃЈ0ЃЌ1ЃЉЛђ
ЃЛЃЈ3ЃЉEЃЈ0ЃЌ1ЃЉЛђ Лђ
Лђ .
.
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAЁЂCЕФзјБъДњШыХзЮяЯпНтЮіЪНПЩЕУГіbЁЂcЕФжЕЃЌМЬЖјЕУГіХзЮяЯпНтЮіЪНЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіACЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉРћгУжсЖдГЦЧѓзюЖЬТЗОЖЕФжЊЪЖЃЌевЕНNЕуЙигкжБЯпx=3ЕФЖдГЦЕуNЁфЃЌСЌНгN'DЃЌN'DгыжБЯпx=3ЕФНЛЕуМДЪЧЕуMЕФЮЛжУЃЌМЬЖјЧѓГіmЕФжЕЃЎ
ЃЈ3ЃЉЩшГіЕуEЕФзјБъЃЌЗжЧщПіЬжТлЃЌЂйЕБЕуEдкЯпЖЮACЩЯЪБЃЌЕуFдкЕуEЩЯЗНЃЌЂкЕБЕуEдкЯпЖЮACЃЈЛђCAЃЉбгГЄЯпЩЯЪБЃЌЕуFдкЕуEЯТЗНЃЌИљОнЦНааЫФБпаЮЕФаджЪБэЪОГіFЕФзјБъЃЌНЋЕуFЕФзјБъДњШыХзЮяЯпНтЮіЪНПЩЕУГіxЕФжЕЃЌМЬЖјЧѓГіЕуEЕФзјБъЃЎ
ЃЈ1ЃЉгЩХзЮяЯпy=-x2+bx+cЙ§ЕуAЃЈ-1ЃЌ0ЃЉМАCЃЈ2ЃЌ3ЃЉЃЌПЩЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЙЪХзЮяЯпЮЊy=-x2+2x+3ЃЌ
ЩшжБЯпACНтЮіЪНЮЊy=kx+nЃЌНЋЕуAЃЈ-1ЃЌ0ЃЉЁЂCЃЈ2ЃЌ3ЃЉДњШыЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЙЪжБЯпACЮЊy=x+1ЃЎ
ЃЈ2ЃЉзїNЕуЙигкжБЯпx=3ЕФЖдГЦЕуNЁфЃЌдђNЁфЃЈ6ЃЌ3ЃЉЃЌгЩЃЈ1ЃЉЕУDЃЈ1ЃЌ4ЃЉЃЌ
ПЩЧѓГіжБЯпDNЁфЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЌ
ЃЌ
ЕБMЃЈ3ЃЌmЃЉдкжБЯпDNЁфЩЯЪБЃЌMN+MDЕФжЕзюаЁЃЌ
дђ![]() ЃЎ
ЃЎ

ЃЈ3ЃЉгЩЃЈ1ЃЉЁЂЃЈ2ЃЉЕУDЃЈ1ЃЌ4ЃЉЃЌBЃЈ1ЃЌ2ЃЉ
ЕуEдкжБЯпACЩЯЃЌЩшEЃЈxЃЌx+1ЃЉЃЌ
ЂйЕБЕуEдкЯпЖЮACЩЯЪБЃЌЕуFдкЕуEЩЯЗНЃЌдђFЃЈxЃЌx+3ЃЉЃЌ
ЁпFдкХзЮяЯпЩЯЃЌ
Ёрx+3=-x2+2x+3
НтЕУЃЌx=0Лђx=1ЃЈЩсШЅЃЉЃЌ
дђЕуEЕФзјБъЮЊЃКЃЈ0ЃЌ1ЃЉЃЎ
ЂкЕБЕуEдкЯпЖЮACЃЈЛђCAЃЉбгГЄЯпЩЯЪБЃЌЕуFдкЕуEЯТЗНЃЌдђFЃЈxЃЌx-1ЃЉЃЌ
ЁпЕуFдкХзЮяЯпЩЯЃЌ
Ёрx-1=-x2+2x+3ЃЌ
НтЕУx=![]() Лђx=
Лђx=![]() ЃЌ
ЃЌ
ЫљвдЃЌy=![]() Лђy=
Лђy=![]()
МДЕуEЕФзјБъЮЊЃКЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
злЩЯПЩЕУТњзуЬѕМўЕФЕуEЮЊEЃЈ0ЃЌ1ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌКЃжагаСНИіаЁЕК![]() ЃЌ
ЃЌ![]() ЃЌФГгцДЌдкКЃжаЕФ
ЃЌФГгцДЌдкКЃжаЕФ![]() ДІВтЕУаЁЕКDЮЛгкЖЋББЗНЯђЩЯЃЌЧвЯрОр
ДІВтЕУаЁЕКDЮЛгкЖЋББЗНЯђЩЯЃЌЧвЯрОр![]() ЃЌИУгцДЌздЮїЯђЖЋКНаавЛЖЮЪБМфЕНДяЕу
ЃЌИУгцДЌздЮїЯђЖЋКНаавЛЖЮЪБМфЕНДяЕу![]() ДІЃЌДЫЪБВтЕУаЁЕК
ДІЃЌДЫЪБВтЕУаЁЕК![]() ЧЁКУдкЕу
ЧЁКУдкЕу![]() ЕФе§ББЗНЯђЩЯЃЌЧвЯрОр
ЕФе§ББЗНЯђЩЯЃЌЧвЯрОр![]() ЃЌгжВтЕУЕу
ЃЌгжВтЕУЕу![]() гыаЁЕК
гыаЁЕК![]() ЯрОр
ЯрОр![]() ЃЎ
ЃЎ
(1)Чѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(2)ЧѓаЁЕК![]() ЃЌ
ЃЌ![]() жЎМфЕФОрРы(МЦЫуЙ§ГЬжаЕФЪ§ОнВЛШЁНќЫЦжЕ)ЃЎ
жЎМфЕФОрРы(МЦЫуЙ§ГЬжаЕФЪ§ОнВЛШЁНќЫЦжЕ)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
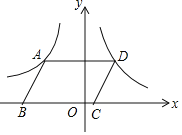
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌABCDЕФЖЅЕуBЃЌCдкxжсЩЯЃЌAЃЌDСНЕуЗжБ№дкЗДБШР§КЏЪ§yЃНЉ![]() ЃЈxЃМ0ЃЉгыyЃН
ЃЈxЃМ0ЃЉгыyЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌШєABCDЕФУцЛ§ЮЊ4ЃЌдђkЕФжЕЮЊЃК_____ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌШєABCDЕФУцЛ§ЮЊ4ЃЌдђkЕФжЕЮЊЃК_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
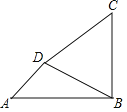
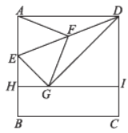
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌPЪЧBCЩЯвЛЖЏЕуЃЌЙ§PзїAPЕФДЙЯпНЛCDгкEЃЌНЋ
ЃЌPЪЧBCЩЯвЛЖЏЕуЃЌЙ§PзїAPЕФДЙЯпНЛCDгкEЃЌНЋ![]() ЗелЕУЕН
ЗелЕУЕН![]() ЃЌбгГЄFPНЛABгкHЃЌСЌНсAEЃЌPEНЛACгкG.
ЃЌбгГЄFPНЛABгкHЃЌСЌНсAEЃЌPEНЛACгкG.
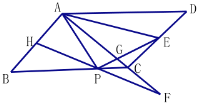
ЃЈ1ЃЉЧѓжЄ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓAEЕФГЄЃЛ
ЪБЃЌЧѓAEЕФГЄЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓAGЕФГЄ.
ЪБЃЌЧѓAGЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗН![]() ЕФБпГЄЮЊ
ЕФБпГЄЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧБп
ЪЧБп![]() ЩЯвЛЕуЃЌ
ЩЯвЛЕуЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЙ§
ЕФжаЕуЃЌЙ§![]() Еузї
Еузї![]() ЃЌЧв
ЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌЙ§
ЃЌЙ§![]() Еузї
Еузї![]() ЃЌЗжБ№НЛ
ЃЌЗжБ№НЛ![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжШчНёЃЌЁАРЌЛјЗжРрЁБвтЪЖвбЩюШыШЫаФЃЌРЌЛјвЛАуПЩЗжЮЊЃКПЩЛиЪеЮяЁЂГјгрРЌЛјЁЂгаКІРЌЛјЁЂЦфЫќРЌЛјЃЎЦфжаМзФУСЫвЛДќРЌЛјЃЌввФУСЫСНДќРЌЛјЃЎ
ЃЈ1ЃЉжБНгаДГіМзЫљФУЕФРЌЛјЧЁКУЪЧЁАГјгрРЌЛјЁБЕФИХТЪЃЛ
ЃЈ2ЃЉЧѓввЫљФУЕФСНДќРЌЛјВЛЭЌРрЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуPЪЧОиаЮABCDЕФБпЩЯвЛЖЏЕуЃЌОиаЮСНБпГЄABЁЂBCГЄЗжБ№ЮЊ15КЭ20ЃЌФЧУДPЕНОиаЮСНЬѕЖдНЧЯпACКЭBDЕФОрРыжЎКЭЪЧЃЈЁЁЁЁЃЉ
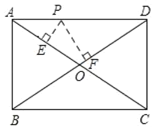
A.6B.12C.24D.ВЛФмШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпyЃНkx+bгыЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкAЃЈ1ЃЌ4ЃЉЁЂBЃЈ4ЃЌ1ЃЉСНЕуЃЌгыxжсНЛгкCЕуЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкAЃЈ1ЃЌ4ЃЉЁЂBЃЈ4ЃЌ1ЃЉСНЕуЃЌгыxжсНЛгкCЕуЃЎ
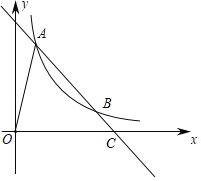
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЭМЯѓжБНгЛиД№ЃКдкЕквЛЯѓЯоФкЃЌЕБxШЁКЮжЕЪБЃЌвЛДЮКЏЪ§жЕДѓгкЗДБШР§КЏЪ§жЕЃП
ЃЈ3ЃЉЕуPЪЧyЃН![]() ЃЈxЃО0ЃЉЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌзїPQЁЭxжсгкQЕуЃЌСЌНгPCЃЌЕБSЁїCPQЃН
ЃЈxЃО0ЃЉЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌзїPQЁЭxжсгкQЕуЃЌСЌНгPCЃЌЕБSЁїCPQЃН![]() SЁїCAOЪБЃЌЧѓЕуPЕФзјБъЃЎ
SЁїCAOЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() гаСНИіВЛЯрЕШЧвЗЧСуЕФЪЕЪ§ИљЃЌЬНОП
гаСНИіВЛЯрЕШЧвЗЧСуЕФЪЕЪ§ИљЃЌЬНОП![]() ТњзуЕФЬѕМўЃЎ
ТњзуЕФЬѕМўЃЎ
аЁЛЊИљОнбЇЯАКЏЪ§ЕФОбщЃЌШЯЮЊПЩвдДгЖўДЮКЏЪ§ЕФНЧЖШбаОПвЛдЊЖўДЮЗНГЬЕФИљЕФЗћКХЁЃЯТУцЪЧаЁЛЊЕФЬНОПЙ§ГЬЃКЕквЛВНЃКЩшвЛдЊЖўДЮЗНГЬ![]() ЖдгІЕФЖўДЮКЏЪ§ЮЊ
ЖдгІЕФЖўДЮКЏЪ§ЮЊ![]() ЃЛ
ЃЛ
ЕкЖўВНЃКНшжњЖўДЮКЏЪ§ЭМЯѓЃЌПЩвдЕУЕНЯргІЕФвЛдЊЖўДЮЗНГЬжа![]() ТњзуЕФЬѕМўЃЌСаБэШчЯТБэЁЃ
ТњзуЕФЬѕМўЃЌСаБэШчЯТБэЁЃ
ЗНГЬСНИљЕФЧщПі | ЖдгІЕФЖўДЮКЏЪ§ЕФДѓжТЭМЯѓ |
|
ЗНГЬгаСНИіВЛЯрЕШЕФИКЪЕИљ |
|
|
Ђй_______ |
|
|
ЗНГЬгаСНИіВЛЯрЕШЕФе§ЪЕИљ | Ђк | Ђл____________ |
ЃЈ1ЃЉЧыНЋБэИёжаЂйЂкЂлВЙГфЭъећЃЛ
ЃЈ2ЃЉвбжЊЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЃЌШєЗНГЬЕФСНИљЖМЪЧе§Ъ§ЃЌЧѓ
ЃЌШєЗНГЬЕФСНИљЖМЪЧе§Ъ§ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com