
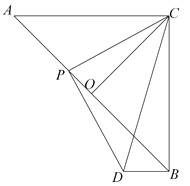
【题目】如图,等腰Rt△ABC的直角边长为![]() ,点O为斜边AB的中点,点P为AB上任意一点,连接PC,以PC为直角边作等腰Rt△PCD,连接BD.
,点O为斜边AB的中点,点P为AB上任意一点,连接PC,以PC为直角边作等腰Rt△PCD,连接BD.
(1)求证: ![]() ;
;
(2)请你判断AC与BD有什么位置关系?并说明理由.
(3)当点P在线段AB上运动时,设AP=x,△PBD的面积为S,求S与x之间的函数关系式.
【答案】(1)见解析; (2) AC与BD平行,详见解析;(3) 当点P在线段AO上时,![]() ;当点P在线段BO上时,
;当点P在线段BO上时,![]() .
.
【解析】
(1)根据△ABC为等腰直角三角形,可推出△BCO为等腰直角三角形,则![]() ,再根据△PCD为等腰直角三角形,得
,再根据△PCD为等腰直角三角形,得![]() ,从而得出结论;
,从而得出结论;
(2)由(1)的结论可得出∠PCO=∠BCD,再由![]() ,可证明△PCO∽△DCB,从而得出∠ABD=∠BAC=45°,根据平行线的判定定理可得出AC∥BD;
,可证明△PCO∽△DCB,从而得出∠ABD=∠BAC=45°,根据平行线的判定定理可得出AC∥BD;
(3)分两种情况讨论:①当点P在线段AO上时,作PE⊥BD,如图1,根据△ABC为等腰直角三角形,得AB=4,PO=2x,BP=4x,根据△PCO∽△DCB,得![]() ,求出BD=
,求出BD=![]() ,再求出
,再求出![]() ,根据三角形面积公式即可得出S与x之间的函数关系式;②当点P在线段BO上时,作PE⊥BD,如图2,可知:OP=x2,BP=4x,再根据△PCO∽△DCB,可得
,根据三角形面积公式即可得出S与x之间的函数关系式;②当点P在线段BO上时,作PE⊥BD,如图2,可知:OP=x2,BP=4x,再根据△PCO∽△DCB,可得![]() ,得出BD=
,得出BD=![]() ,求出PE=
,求出PE=![]() ,根据三角形面积公式即可得出S与x之间的函数关系式.
,根据三角形面积公式即可得出S与x之间的函数关系式.
解:(1)∵△ABC为等腰直角三角形,O是AB的中点,
∴∠OCB=∠CBO=45°,∠COB=∠AOC=90°,
∴△BCO为等腰直角三角形,
∴![]() ,
,
∵△PCD为等腰直角三角形
∴![]() ,
,
∴![]() ;
;
(2) AC∥BD,
理由:由(1)可知:∠PCO+∠OCD=∠BCD+∠OCD=45°,
∴∠PCO=∠BCD,
又∵![]() ,
,
∴△PCO∽△DCB,
∴∠CBD=∠AOC=90°,
∴∠ABD=∠BAC=45°,
∴AC∥BD;
(3)分两种情况讨论:
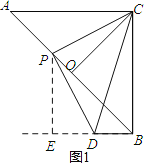
①当点P在线段AO上时,作PE⊥BD,如图1,
∵AC=BC=![]() ,△ABC为等腰直角三角形,
,△ABC为等腰直角三角形,
∴AB=4,则AO=BO=CO=2,
∴PO=2﹣x,BP=4﹣x,
∵△PCO∽△DCB,
∴![]() ,即
,即![]() ,
,
∴BD=![]() ,
,
∵∠PBE=45°,
∴![]() ,
,
∴![]() ;
;
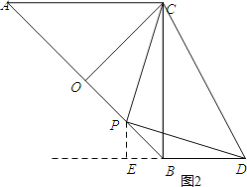
②当点P在线段BO上时,作PE⊥BD,如图2,
可知:OP=x﹣2,BP=4﹣x,
∵△PCO∽△DCB,
∴![]() ,即
,即![]() ,
,
∴BD=![]() ,
,
∵∠PBE=45°,
∴![]() ,
,
∴![]() .
.
综上所述:当点P在线段AO上时,![]() ;当点P在线段BO上时,
;当点P在线段BO上时,![]() .
.


科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,篮球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机,再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕AO与边BC交于点O,连结AP、OP.
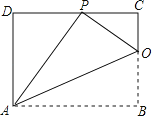
(1)求证:△PDA∽△OCP;
(2)若tan∠PAO=![]() ,求CP的长.
,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b= ,
,
例如:1⊕(﹣3)=![]() =﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
=﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
(x2+1)⊕(x﹣1)=![]() (因为x2+1>0)
(因为x2+1>0)
参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>![]() ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1M1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn的面积为Sn,则Sn= .(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
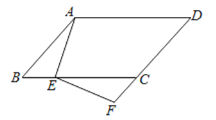
(1) 求证:△ABE∽△ECF;
(2) 若AB=5,AD=8,BE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于M,N两点(点M在点N的左侧),其顶点P在线段AB上移动,点A,B的坐标分别为(-2,-3),(1,-3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )

A.-1 B.-3C.-5D.-7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com