练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
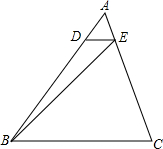
    如图，在△ABC中，D、E分别是AB、AC上的点，且DE∥BC，如果AE：EC=1：4，那么S△ADE：S△EBC=（　　）
    A、1：24B、1：20
    C、1：18D、1：16
    考点：相似三角形的判定与性质
    专题：
    分析：由已知条件可求得
    S△ABE
    S△EBC
    ，又由平行线分线段成比例可求得
    S△ADE
    S△BDE
    ，结合S△BDE=S△ABE-S△ADE可求得答案．
    解答：解：∵
    AE
    EC
    =
    1
    4
    ，
    ∴
    S△ABE
    S△EBC
    =
    1
    4
    ，
    ∴S△ABE=
    1
    4
    S△EBC，
    ∵DE∥BC，
    ∴
    AD
    DB
    =
    AE
    EC
    =
    1
    4
    ，
    ∴
    S△ADE
    S△BDE
    =
    1
    4
    ，
    ∴S△BDE=4S△ADE，
    又∵S△BDE=S△ABE-S△ADE，
    ∴4S△ADE=
    1
    4
    S△EBC-S△ADE，
    ∴
    S△ADE
    S△EBC
    =
    1
    20
    ，
    故选B．
    点评：本题主要考查平行线分线段成比例的性质及三角形的面积，掌握同高三角形的面积比即为底的比是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    根据六年级学生参加拓展课程情况绘制了两幅不完整的统计图（如图）已知参加摄影与音乐学科学生人数比为2：3，请根据统计图提供的信息，解答下列问题：
    （1）参加拓展课程学习的学生总数是
     
    ；
    （2）把两幅统计图补充完整．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

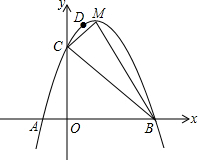    如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，其中A点坐标为（-1，0），点C（0，5），D（1，8）在抛物线上，M为抛物线的顶点．
    （1）抛物线的解析式为
     
    ；
    （2）△MCB的面积为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

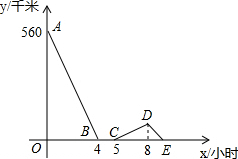    一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后都停留一段时间，然后分别按原速一同驶往甲地后停车．设慢车行驶的时间为x小时，两车之间的距离为y千米，图中折线表示y与x之间的函数图象，下列四种说法：
    ①甲乙两地之间的距离为560千米；
    ②快车的速度是80千米/时；
    ③慢车的速度是60千米/时；
    ④线段DE所表示的y与x之间的函数关系式为y=-60x+540．
    其中正确的个数是（　　）
    A、1个B、2个C、3个D、4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，正方形ABCD绕点A逆时针旋转，得到正方形AB′C′D′，当两正方形重叠部分的面积是原正方形面积的
    1
    4
    时，sin
    1
    2
    ∠B′AD=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    “知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技运动会．如图为我市某校2012年参加科技运动会航模比赛（包括空模、海模、车模、建模四个类别）的参赛人数统计图：
    （1）该校参加车模、建模比赛的人数分别是
     
    人和
     
    人；
    （2）该校参加航模比赛的总人数是
     
    人；
    （3）空模所在扇形的圆心角的度数是
     
    °，并把条形统计图补充完整：（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）；
    （4）从全市中小学参加航模比赛选手中随机抽取80人，其中有32人获奖．今年我市中小学参加航模比赛人数共有2100人，请你估算今年参加航模比赛的获奖人数约是多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕着点C旋转90°，点A、B的对应点分别是D、E，那么tan∠ADE的值
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知AB∥CD∥EF，它们依次交直线l1、l2于点A、D、F和点B、C、E，如果AD=6，DF=3，BC=5，那么BE=
     
    ．

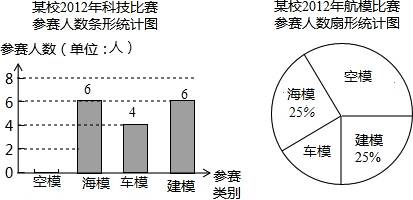
    查看答案和解析>>

    科目：初中数学 来源： 题型：

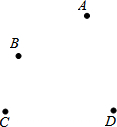    如图，平面上四个点A，B，C，D．按要求完成下列问题：
    （1）连接AD，BC；
    （2）画射线AB与直线CD相交于E点；
    （3）用量角器度量得∠AED的大小为
     
    （精确到度）．

    查看答案和解析>>

    同步练习册答案