
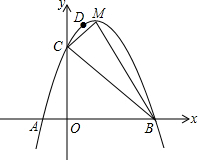
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),D(1,8)在抛物线上,M为抛物线的顶点.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),D(1,8)在抛物线上,M为抛物线的顶点.| 1 |
| 2 |
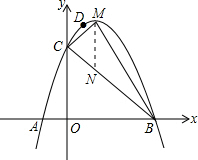 解:(1)∵A(-1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
解:(1)∵A(-1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
|
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
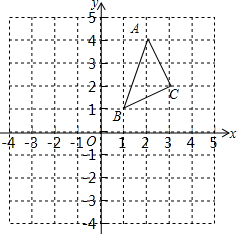 △ABC在平面直角坐标系中的位置如图所示(A、B、C三点在格点上),把△ABC绕原点O顺时针旋转90°,A、B、C旋转后的对应点分别是A1、B1、C1
△ABC在平面直角坐标系中的位置如图所示(A、B、C三点在格点上),把△ABC绕原点O顺时针旋转90°,A、B、C旋转后的对应点分别是A1、B1、C1查看答案和解析>>
科目:初中数学 来源: 题型:
 某校准备在校内倡导“光盘行动”,随机调查了部分同学某年餐后饭菜的剩余情况,调查数据的部分统计结果如表:
某校准备在校内倡导“光盘行动”,随机调查了部分同学某年餐后饭菜的剩余情况,调查数据的部分统计结果如表:| 项目 | 人数 | 百分比 |
| 没有剩 | 80 | 40% |
| 剩少量 | a | 20% |
| 剩一半 | 50 | b |
| 剩大量 | 30 | 15% |
| 合计 | 200 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:
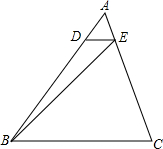 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AE:EC=1:4,那么S△ADE:S△EBC=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AE:EC=1:4,那么S△ADE:S△EBC=( )| A、1:24 | B、1:20 |
| C、1:18 | D、1:16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、4 | B、5 | C、6 | D、3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com