
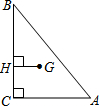
 如图,已知在△ABC中,∠ACB=90°,AC=6,点G为重心,GH⊥BC,垂足为点H,那么GH=
如图,已知在△ABC中,∠ACB=90°,AC=6,点G为重心,GH⊥BC,垂足为点H,那么GH=| 1 |
| 2 |
| BG |
| BD |
| 2 |
| 3 |
| GH |
| DC |
| BG |
| BD |
| 2 |
| 3 |
| 2 |
| 3 |
 解:连结BG并延长交AC于点D.
解:连结BG并延长交AC于点D.| 1 |
| 2 |
| BG |
| BD |
| 2 |
| 3 |
| GH |
| DC |
| BG |
| BD |
| 2 |
| 3 |
| 2 |
| 3 |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,方格纸中的每个小方个都是边长为一个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
如图,方格纸中的每个小方个都是边长为一个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
已知:如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.查看答案和解析>>
科目:初中数学 来源: 题型:
 某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为50米的篱笆围成.已知墙长为26米(如图所示),设这个苗圃园平行于墙的一边的长为x米.
某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为50米的篱笆围成.已知墙长为26米(如图所示),设这个苗圃园平行于墙的一边的长为x米.查看答案和解析>>
科目:初中数学 来源: 题型:
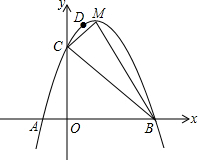 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),D(1,8)在抛物线上,M为抛物线的顶点.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),D(1,8)在抛物线上,M为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:
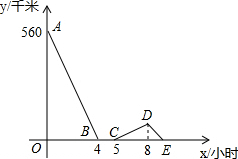 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,下列四种说法:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,下列四种说法:| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com