
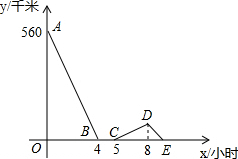
 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,下列四种说法:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,下列四种说法:| A、1个 | B、2个 | C、3个 | D、4个 |
|
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 水果品牌 | A | B | C |
| 每辆汽车载重量(吨) | 6 | 5 | 4 |
| 每吨水果可获利润(万元) | 0.5 | 0.6 | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某校准备在校内倡导“光盘行动”,随机调查了部分同学某年餐后饭菜的剩余情况,调查数据的部分统计结果如表:
某校准备在校内倡导“光盘行动”,随机调查了部分同学某年餐后饭菜的剩余情况,调查数据的部分统计结果如表:| 项目 | 人数 | 百分比 |
| 没有剩 | 80 | 40% |
| 剩少量 | a | 20% |
| 剩一半 | 50 | b |
| 剩大量 | 30 | 15% |
| 合计 | 200 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:
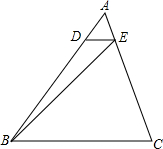 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AE:EC=1:4,那么S△ADE:S△EBC=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AE:EC=1:4,那么S△ADE:S△EBC=( )| A、1:24 | B、1:20 |
| C、1:18 | D、1:16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com