Question

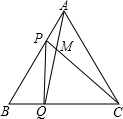
如图，点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点（其中P、Q不与端点重合），点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，连接AQ、CP交于点M，则在P、Q运动的过程中，下列结论：（1）BP=CM；（2）△ABQ≌△CAP；（3）∠CMQ的度数始终等于60°；（4）当第

4

3

秒或第

8

3

秒时，△PBQ为直角三角形．其中正确的结论有（　　）

• A、1个
• B、2个
• C、3个
• D、4个

Answer 1

考点：全等三角形的判定与性质,等边三角形的性质

专题：

分析：易证△ABQ≌△CAP，可得∠AQB=∠CPA，即可求得∠AMP=∠B=60°，易证∠CQM≠60°，可得CQ≠CM，根据t的值易求BP，BQ的长，即可求得PQ的长，即可解题．

解答：解：∵△ABC是等边三角形，
∴AB=BC=AC，∠BAC=∠B=∠ACB=60°，
根据题意得：AP=BQ，
在△ABQ和△CAP中，

AB=AC ∠B=∠CAP BQ=AP

，
∴△ABQ≌△CAP（SAS），（2）正确；
∴∠AQB=∠CPA，
∵∠BAQ+∠APC+∠AMP=180°，∠BAQ+∠B+∠AQB=180°，
∴∠AMP=∠B=60°，
∴∠QMC=60°，（3）正确；
∵∠QMC=60°，∠QCM≠60°，
∴∠CQM≠60°，
∴CQ≠CM，
∵BP=CQ，
∴CM≠BP，（1）错误；
当t=

4

3

时，BQ=

4

3

，BP=4-

4

3

=

8

3

，

∵PQ²=BP²+BQ²-2BP•BQcos60°，
∴PQ=

4 3

3

，
∴△PBQ为直角三角形，
同理t=

8

3

时，△PBQ为直角三角形仍然成立，（4）正确；
故选 C．

点评：本题考查了全等三角形的判定，考查了全等三角形对应边、对应角相等的性质，本题中求证△ABQ≌△CAP是解题的关键．