
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的顶点A(-3,0),与y轴交于点B(0,4),在第一象限内有一点P(m,n),且满足4m+3n=12.
(1)求二次函数解析式.
(2)若以点P为圆心的圆与直线AB、x轴相切,求点P的坐标.
(3)若点A关于y轴的对称点为点A′,点C在对称轴上,且2∠CBA+∠PA′O=90.求点C的坐标.
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,
,![]() );(3)C(-3,-5)或 (-3,
);(3)C(-3,-5)或 (-3,![]() )
)
【解析】
(1)设顶点式,将B点代入即可求;
(2)根据4m+3n=12确定点P所在直线的解析式,再根据内切线的性质可知P点在∠BAO的角平分线上,求两线交点坐标即为P点坐标;
(3)根据角之间的关系确定C在∠DBA的角平分线与对称轴的交点或∠ABO的角平分线与对称轴的交点,通过求角平分线的解析式即可求.
(1)∵抛物线的顶点坐标为A(-3,0),
设二次函数解析式为y=a(x+3)2,
将B(0,4)代入得,4=9a
∴a=![]()
∴![]()
(2)如图
∵P(m,n),且满足4m+3n=12
∴![]()
∴点P在第一象限的![]() 上,
上,
∵以点P为圆心的圆与直线AB、x轴相切,
∴点P在∠BAO的角平分线上,
∠BAO的角平分线:y=![]() ,
,
∴![]()
![]() ,
,
∴x=![]() ,∴y=
,∴y=![]()
∴P(![]() ,
,![]() )
)
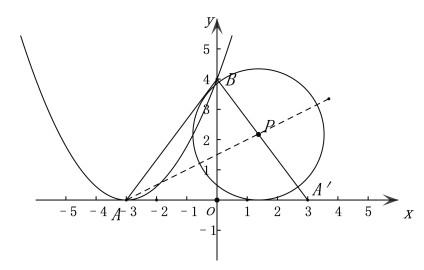
(3)C(-3,-5)或 (-3,![]() )理由如下:
)理由如下:
如图,A(3,0),可得直线LAB的表达式为![]() ,
,
∴P点在直线AB上,
∵∠PAO=∠ABO=∠BAG, 2∠CBA+∠PA′O=90°,
∴2∠CBA=90°-∠PA′O=∠GAB,
在对称轴上取点D,使∠DBA=∠DAB,作BE⊥AG于G点,
设D点坐标为(-3,t) 则有(4-t)2+32=t2 t= ∴D(-3, 作∠DBA的角平分线交AG于点C即为所求点,设为C1 ∠DBA的角平分线BC1的解析式为y= ∴C1的坐标为 (-3, 同理作∠ABO的角平分线交AG于点C即为所求,设为C2, ∠ABO的角平分线BC2的解析式为y=3x+4, ∴C2的坐标为(-3,-5). 综上所述,点C的坐标为(-3, ![]() ,
,![]() ),
),![]() x+4,
x+4,![]() );
);![]() )或(-3,-5).
)或(-3,-5).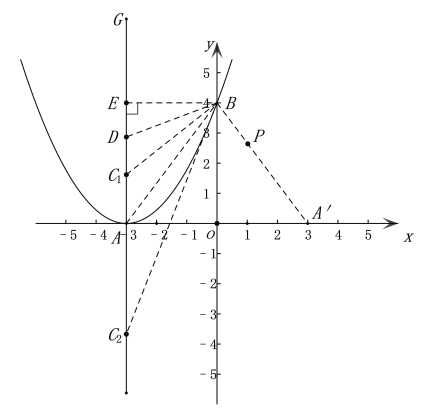


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解后面的问题.
材料:一个三位自然数![]() (百位数字为a,十位数字为b,个位数字为c),若满足a+c=b,则称这个三位数为“欢喜数”,并规定F(
(百位数字为a,十位数字为b,个位数字为c),若满足a+c=b,则称这个三位数为“欢喜数”,并规定F(![]() )=ac.如374,因为它的百位上数字3与个位数字4之和等于十位上的数字7,所以374是“欢喜数”,∴F(374)=3×4=12.
)=ac.如374,因为它的百位上数字3与个位数字4之和等于十位上的数字7,所以374是“欢喜数”,∴F(374)=3×4=12.
(1)对于“欢喜数![]() ”,若满足b能被9整除,求证:“欢喜数
”,若满足b能被9整除,求证:“欢喜数![]() ”能被99整除;
”能被99整除;
(2)已知有两个十位数字相同的“欢喜数”m,n(m>n),若F(m)﹣F(n)=3,求m﹣n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
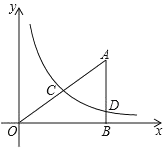
【题目】如图,已知Rt△ABO,点B在![]() 轴上,∠ABO=90°,∠AOB=30°,OB=
轴上,∠ABO=90°,∠AOB=30°,OB=![]() ,反比例函数
,反比例函数![]() 的图象经过OA的中点C,交AB于点D.
的图象经过OA的中点C,交AB于点D.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求△OCD的面积;
(3)点P是![]() 轴上的一个动点,请直接写出使△OCP为直角三角形的点P坐标.
轴上的一个动点,请直接写出使△OCP为直角三角形的点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
【1】从A、D、E、F四点中任意取一点,以所取的这一点及B、C为顶点三角形,则所画三角形是等腰三角形的概率是 ▲ ;
【2】从A、D、E、F四点中先后任意取两个不同的点,以所取的这两点及B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表求解).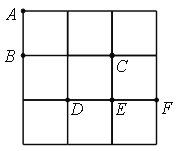
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
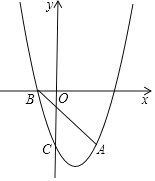
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一点P,使PB+PC的值最小,求点P的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系:
y=![]()
(1)李明第几天生产的粽子数量为280只?
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
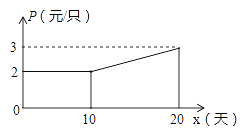
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为3的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,4)经过点O、点C作直线l,将直线l沿y轴上下平移.
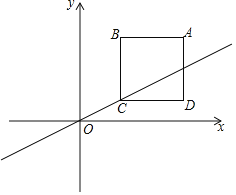
(1)当直线l与正方形ABCD只有一个公共点时,求直线l的解析式;
(2)当直线l在平移过程中恰好平分正方形ABCD的面积时,直线l分别与x轴、y轴相交于点E、点F,连接BE、BF,求△BEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com