
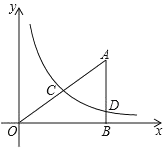
【题目】如图,已知Rt△ABO,点B在![]() 轴上,∠ABO=90°,∠AOB=30°,OB=
轴上,∠ABO=90°,∠AOB=30°,OB=![]() ,反比例函数
,反比例函数![]() 的图象经过OA的中点C,交AB于点D.
的图象经过OA的中点C,交AB于点D.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求△OCD的面积;
(3)点P是![]() 轴上的一个动点,请直接写出使△OCP为直角三角形的点P坐标.
轴上的一个动点,请直接写出使△OCP为直角三角形的点P坐标.
【答案】(1)![]() ;(2)面积为
;(2)面积为![]() ;(3)P(2,0)或(4,0)
;(3)P(2,0)或(4,0)
【解析】
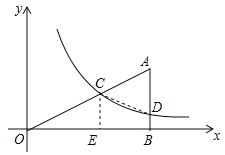
(1)解直角三角形求得AB,作CE⊥OB于E,根据平行线分线段成比例定理和三角形中位线的性质求得C的坐标,然后根据待定系数法即可求得反比例函数的解析式;
(2)补形法,求出各点坐标,S△OCD =S△AOB-S△ACD- S△OBD;
(3)分两种情形:①∠OPC=90°.②∠OCP=90°,分别求解即可.
解:(1)∵∠ABO=90°,∠AOB=30°,OB=![]() ,
,
∴AB=![]() OB=2,
OB=2,
作CE⊥OB于E,
∵∠ABO=90°,
∴CE∥AB,
∴OC=AC,
∴OE=BE=![]() OB=
OB=![]() ,CE=
,CE=![]() AB=1,
AB=1,
∴C(![]() ,1),
,1),
∵反比例函数![]() (x>0)的图象经过OA的中点C,
(x>0)的图象经过OA的中点C,
∴1=![]() ,∴k=
,∴k=![]() ,
,
∴反比例函数的关系式为![]() ;
;
(2)∵OB=![]() ,
,
∴D的横坐标为![]() ,
,
代入![]() 得,y=
得,y=![]() ,
,
∴D(![]() ,
,![]() ),
),
∴BD=![]() ,
,
∵AB=![]() ,
,
∴AD=![]() ,
,
∴S△OCD =S△AOB-S△ACD- S△OBD =![]() OBAB-
OBAB-![]() ADBE-
ADBE-![]() BDOB=
BDOB=![]()
(3)当∠OPC=90°时,点P的横坐标与点C的横坐标相等,C(2,2),
∴P(2,0).
当∠OCP=90°时.
∵C(2,2),
∴∠COB=45°.
∴△OCP为等腰直角三角形.
∴P(4,0).
综上所述,点P的坐标为(2,0)或(4,0).


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】有四组家庭参加亲子活动,A、B、C、D分别代表四个家长,他们的孩子分别是a、b、c、d,若主持人随机从家长、孩子中各选择一个,请你用树状图或列表的方法求出选中的两人刚好是同一个家庭的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
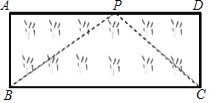
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
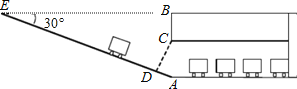
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,分析下列四个结论:①abc<0;②b2-4ac>0;③
的图象如图所示,分析下列四个结论:①abc<0;②b2-4ac>0;③![]() ;④a+b+c<0.其中正确的结论有( )
;④a+b+c<0.其中正确的结论有( )
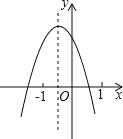
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是以点A为圆心2为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最小值为__________.
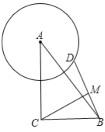
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的顶点A(-3,0),与y轴交于点B(0,4),在第一象限内有一点P(m,n),且满足4m+3n=12.
(1)求二次函数解析式.
(2)若以点P为圆心的圆与直线AB、x轴相切,求点P的坐标.
(3)若点A关于y轴的对称点为点A′,点C在对称轴上,且2∠CBA+∠PA′O=90.求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图甲是小张同学设计的带图案的花边作品,该作品由形如图乙的矩形图案设计拼接面成(不重叠,无缝隙).图乙中,点E、F、G、H分别为矩形AB、BC、CD、DA的中点,若AB=4,BC=6,则图乙中阴影部分的面积为
_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解今年九年级学生的数学学习情况,在中考考前适应性训练测试后,对九年级全体同学的数学成绩作了统计分析,按照成绩高低分为A、B、C、D四个等级并绘制了如图1和图2的统计图(均不完整),请结合图中所给出的信息解答问题:
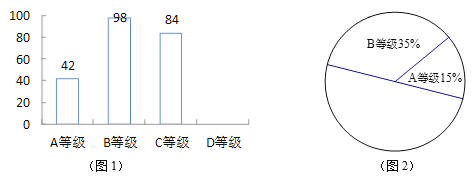
(1)该校九年级学生共有 人.
(2)补全条形统计图与扇形统计图.(要求:请将扇形统计图的空白部分按比例分成两部分.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com