
【题目】图甲是小张同学设计的带图案的花边作品,该作品由形如图乙的矩形图案设计拼接面成(不重叠,无缝隙).图乙中,点E、F、G、H分别为矩形AB、BC、CD、DA的中点,若AB=4,BC=6,则图乙中阴影部分的面积为
_____.

【答案】![]()
【解析】
根据S阴=S菱形PHQF﹣2S△HTN,再求出菱形PHQF的面积,△HTN的面积即可解决问题.
如图,设FM=HN=a.
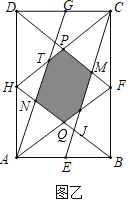
由题意点E、F、G、H分别为矩形AB、BC、CD、DA的中点,
∴四边形DFBH和四边形CFAH为平行四边形,
∴DF∥BH,CH∥AF,
∴四边形HQFP是平行四边形
又HP=![]() CH=DP=PF,
CH=DP=PF,
∴平行四边形HQFP是菱形,它的面积=![]() S矩形ABCD=
S矩形ABCD=![]() ×4×6=6,
×4×6=6,
∵FM∥BJ,CF=FB,
∴CM=MJ,
∴BJ=2FM=2a,
∵EJ∥AN,AE=EB,
∴BJ=JN=2a,
∵S△HBC=![]() 64=12,HJ=
64=12,HJ=![]() BH,
BH,
∴S△HCJ=![]() ×12=
×12=![]() ,
,
∵TN∥CJ,
∴△HTN∽△HCJ,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∴S△HTN=![]() ×
×![]() =
=![]() ,
,
∴S阴=S菱形PHQF﹣2S△HTN=6﹣![]() =
=![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
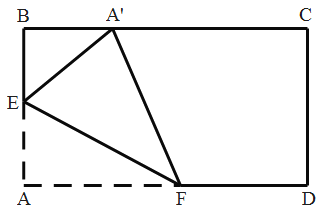
【题目】如图,矩形纸片ABCD中,AB=6cm,AD=10cm,点E、F在矩形ABCD的边AB、AD上运动,将△AEF沿EF折叠,使点A′在BC边上,当折痕EF移动时,点A′在BC边上也随之移动.则A′C的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
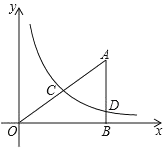
【题目】如图,已知Rt△ABO,点B在![]() 轴上,∠ABO=90°,∠AOB=30°,OB=
轴上,∠ABO=90°,∠AOB=30°,OB=![]() ,反比例函数
,反比例函数![]() 的图象经过OA的中点C,交AB于点D.
的图象经过OA的中点C,交AB于点D.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求△OCD的面积;
(3)点P是![]() 轴上的一个动点,请直接写出使△OCP为直角三角形的点P坐标.
轴上的一个动点,请直接写出使△OCP为直角三角形的点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
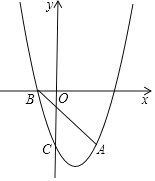
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一点P,使PB+PC的值最小,求点P的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
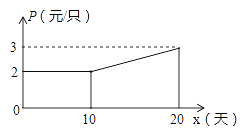
【题目】传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系:
y=![]()
(1)李明第几天生产的粽子数量为280只?
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴分别交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)如图1,求△BCD的面积;
(2)如图2,P是抛物线BD段上一动点,连接CP并延长交x轴于E,连接BD交PC于F,当△CDF的面积与△BEF的面积相等时,求点E和点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为﹣3和1;④b2﹣4ac>0,其中正确的命题有( )
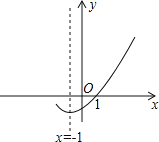
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级一班和二班各派出10名学生参加一分钟跳绳比赛,成绩如下表:
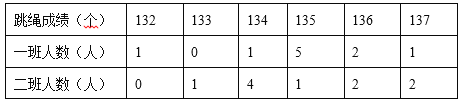
(1)两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表:
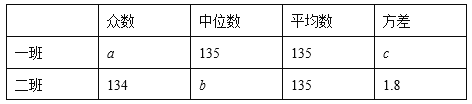
表中数据a= ,b= ,c= .
(2)请用所学的统计知识,从两个角度比较两个班跳绳比赛的成绩.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com