
如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
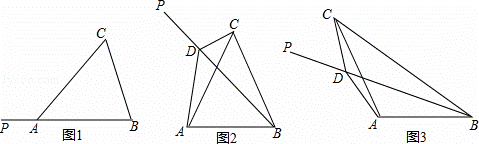
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=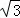 AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
解:(1)如图2,∵∠CDP=120°,
∴∠CDB=60°,
∵∠BAC=60°,
∴∠CDB=∠BAC=60°,
∴A、B、C、D四点共圆,
∴∠ACD=∠ABD.
在BP上截取BE=CD,连接AE.
在△DCA与△EBA中,
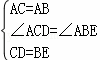 ,
,
∴△DCA≌△EBA(SAS),
∴AD=AE,∠DAC=∠EAB,
∵∠CAB=∠CAE+∠EAB=60°,
∴∠DAE=60°,
∴△ADE是等边三角形,
∴DE=AD.
∵BD=BE+DE,
∴BD=CD+AD.
故答案为=,BD=CD+AD;
(2)如图3,设AC与BD相交于点O,在BP上截取BE=CD,连接AE,过A作AF⊥BD于F.
∵∠CDP=60°,
∴∠CDB=120°.
∵∠CAB=120°,
∴∠CDB=∠CAB,
∵∠DOC=∠AOB,
∴△DOC∽△AOB,
∴∠DCA=∠EBA.
在△DCA与△EBA中,
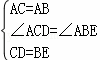 ,
,
∴△DCA≌△EBA(SAS),
∴AD=AE,∠DAC=∠EAB.
∵∠CAB=∠CAE+∠EAB=120°,
∴∠DAE=120°,
∴∠ADE=∠AED=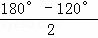 =30°.
=30°.
∵在Rt△ADF中,∠ADF=30°,
∴DF= AD,
AD,
∴DE=2DF=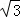 AD,
AD,
∴BD=DE+BE=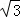 AD+CD,
AD+CD,
∴BD﹣CD=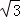 AD;
AD;
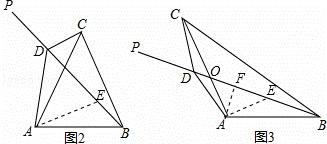
(3)BD+CD=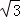 AD.
AD.


科目:初中数学 来源: 题型:
某中学为开拓学生视野,开展“课外读 书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
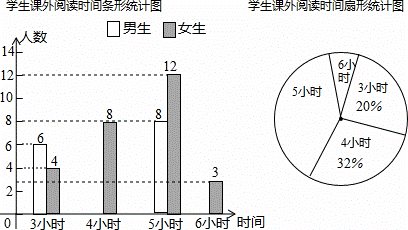
(1)本次调查的学生总数为 人,被调查学生的课外阅读时间的中位数是 小时,众数是 小时;
(2)请你补全条形统计图;
(3)在扇形统计图中,课 外阅读时间为5小时的扇形的圆心角度数是 ;
外阅读时间为5小时的扇形的圆心角度数是 ;
(4)若全校九年级共有学生700人,估计九年级一周课外阅读时间为6小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
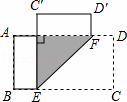
如图,在矩形ABCD中,AB=6cm,点E、F分别是边BC、AD上一点,将矩形ABCD沿EF折叠,使点C、D分别落在点C′、D′处.若C′E⊥AD,则EF的长为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com