
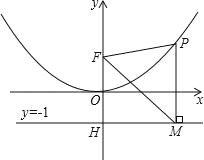
【题目】二次函数图象的顶点在原点O,经过点A(1,![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
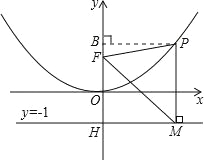
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
【答案】(1)二次函数的解析式为y=![]() x2;(2)证明见试题解析;(3)满足条件的点P的坐标为(2
x2;(2)证明见试题解析;(3)满足条件的点P的坐标为(2![]() ,3)或(﹣2
,3)或(﹣2![]() ,3).
,3).
【解析】
试题分析:(1)根据题意可设函数的解析式为y=ax2,将点A代入函数解析式,求出a的值,继而可求得二次函数的解析式;
(2)过点P作PB⊥y轴于点B,利用勾股定理求出PF,表示出PM,可得PF=PM,∠PFM=∠PMF,结合平行线的性质,可得出结论;
(3)首先可得∠FMH=30°,设点P的坐标为(x,![]() x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.
x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.
试题解析:(1)∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1,![]() )代入y=ax2得:a=
)代入y=ax2得:a=![]() ,
,
∴二次函数的解析式为y=![]() x2;
x2;
(2)∵点P在抛物线y=![]() x2上,
x2上,
∴可设点P的坐标为(x,![]() x2),
x2),
过点P作PB⊥y轴于点B,则BF=|![]() x2﹣1|,PB=|x|,
x2﹣1|,PB=|x|,
∴Rt△BPF中,
PF=![]() =
=![]() x2+1,
x2+1,
∵PM⊥直线y=﹣1,
∴PM=![]() x2+1,
x2+1,
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥y轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP;
(3)当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴![]() x2+1=4,
x2+1=4,
解得:x=±2![]() ,
,
∴![]() x2=
x2=![]() ×12=3,
×12=3,
∴满足条件的点P的坐标为(2![]() ,3)或(﹣2
,3)或(﹣2![]() ,3).
,3).


科目:初中数学 来源: 题型:
【题目】到三角形三顶点距离相等的点是( ),到三角形三边距离相等的点是( )
A. 三条角平分线的交点,三条垂直平分线的交点
B. 三条角平分线的交点,三条中线的交点
C. 三条垂直平分线的交点,三条中线的交点
D. 三条垂直平分线的交点,三条角平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先观察下面的解题过程,然后解答问题:
题目:化简:(2+1)(22+1)(24+1)
解:
(2+1)(22+1)(24+1)
=(2﹣1)(2+1)(22+1)(24+1)
=(22﹣1)(22+1)(24+1)
=(24﹣1)(24+1)
=28﹣1.
问题:
(1)化简(2+1)(22+1)(24+1)(28+1)…(264+1).
(2)求(3+1)(32+1)(34+1)(38+1)…(3n+1)﹣ ![]() (n可以写成2n的形式,k为正整数)的值.
(n可以写成2n的形式,k为正整数)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程月1026千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到
当日8:40从烟台到该是的高铁票,而且从该市火车站到会议地点最多需要1.5小时.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
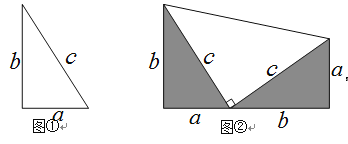
【题目】(10分)图②是一个直角梯形.该图案可以看作由2个边长为a、b、c的直角三角形(图①)和1个腰长为c的等腰直角三角形拼成。
(1)根据图②和梯形面积的不同计算方法,可以验证一个含a、b、c的等式,请你写出这个等式,并写出其推导过程;
(2)若直角三角形的边长a、b、c满足条件:a―b=1, ab=4.试求出c的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对代数式x2﹣1的意义,下列说法不正确的是( )
A. x与1的差的平方 B. x的平方与1的差 C. x与1的平方差 D. 比x的平方少1的数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,那么每年投资的增长率为( )
A.20%
B.40%
C.-220%
D.30%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=﹣![]() x﹣1与反比例函数y2=
x﹣1与反比例函数y2=![]() 的图象交于点A(﹣4,m).
的图象交于点A(﹣4,m).
(1)观察图象,在y轴的左侧,当y1>y2时,请直接写出x的取值范围;
(2)求出反比例函数的解析式.
(3)求直线与双曲线的另一个交点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com