
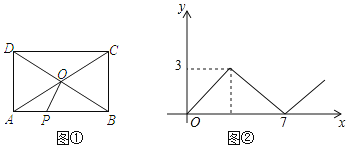
【题目】如图①,在矩形ABCD中,AB>AD,对角线AC、BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动,设点P的运动路径为x,△AOP的面积为y,图②是y关于x的函数关系图象,则AB边的长为( )
A. 3B. 4C. 5D. 6
【答案】B
【解析】
根据图形,分情况当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,△AOP面积最大为3,推出ABBC=12;当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,可推出AB.
解:当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,△AOP面积最大为3.
∴![]() AB
AB![]() BC=3,即ABBC=12.
BC=3,即ABBC=12.
当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,
∴AB+BC=7.
则BC=7﹣AB,代入ABBC=12,得AB2﹣7AB+12=0,解得AB=4或3,
因为AB>BC,所以AB=4.
故选:B.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】“六一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法:①当n很大时,估计指针落在“铅笔”区域的频率大约是0.70;②假如你去转动转盘一次,获得铅笔的概率大约是0.70;③如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次;④转动转盘10次,一定有3次获得文具盒.中正确的是_____
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )

A. 2017π B. 2034π C. 3024π D. 3026π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b与双曲线![]() (x﹤0)相交于A(-4,a)、B(-1,4)两点.
(x﹤0)相交于A(-4,a)、B(-1,4)两点.

(1)求直线和双曲线的解析式;
(2)在y轴上存在一点P,使得PA+PB的值最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
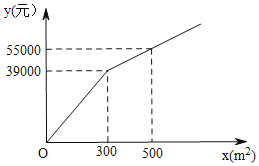
【题目】为了美化环境,建设宜居衡阳,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)求y与x的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1000m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的3倍,那么应该怎忙分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
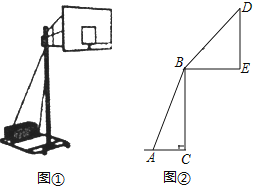
【题目】如图①,②分别是某款篮球架的实物图和示意图,已知支架AB的长为2.3m,支架AB与地面的夹角∠BAC=70°,BE的长为1.5m,篮板部支架BD与水平支架BE的夹角为46°,BC、DE垂直于地面,求篮板顶端D到地面的距离.(结果保留一位小数,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲节即将到来之际,某商店准备购进![]() 、
、![]() 两种男装进行销售,其中每套
两种男装进行销售,其中每套![]() 种男装的进价比每套
种男装的进价比每套![]() 种男装的进价多
种男装的进价多![]() 元用
元用![]() 元购进
元购进![]() 种男装的数量是用
种男装的数量是用![]() 元购进
元购进![]() 种男装数量的
种男装数量的![]() 倍.
倍.
(1)求每套![]() 种男装和每套
种男装和每套![]() 种男装的进价各是多少元:
种男装的进价各是多少元:
(2)若该商店本次购进![]() 种男装的数量比购进
种男装的数量比购进![]() 种男装的数量的
种男装的数量的![]() 倍还多
倍还多![]() 套,该商店每套
套,该商店每套![]() 种男装的销售价格为
种男装的销售价格为![]() 元,每套
元,每套![]() 种男装的销售价格为
种男装的销售价格为![]() 元,若将本次购进的
元,若将本次购进的![]() 、
、![]() 两种男装全部售出后获得的利润不少于
两种男装全部售出后获得的利润不少于![]() 元,那么该商店至少需要购进
元,那么该商店至少需要购进![]() 种男装多少套?
种男装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
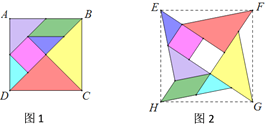
【题目】七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”.下面的两幅图正方形(如图1)、“风车型”(如图2)都是由同一副七巧板拼成的,则图中正方形ABCD,EFGH的面积比为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
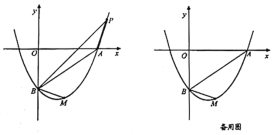
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com