
【题目】如图,△ABC内接于⊙O,AC=BC,CD是⊙O的直径,与AB相交于点G,过点D作EF∥AB,分别交CA、CB的延长线于点E、F,连接BD.
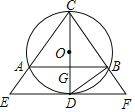
(1)求证:EF是⊙O的切线;
(2)求证:BD2=ACBF.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据圆的对称性可得∠ACD=∠BCD,根据等腰三角形的性质可得CD⊥AB,由EF//AB可得∠CDF=∠CGB=90°,即可得答案;(2)先证明△BCD∽△BDF,利用相似三角形的性质可知:![]() ,利用BC=AC即可求证BD2=ACBF.
,利用BC=AC即可求证BD2=ACBF.
(1)∵AC=BC,CD是圆的直径,
∴由圆的对称性可知:∠ACD=∠BCD,
∴CD⊥AB,
∵AB∥EF,
∴∠CDF=∠CGB=90°,
∵OD是圆的半径,
∴EF是⊙O的切线;
(2)∵∠BDF+∠CDB=∠CDB+∠C=90°,
∴∠BDF=∠CDB,
∴△BCD∽△BDF,
∴![]() ,
,
∴BD2=BCBD,
∵BC=AC,
∴BD2=ACBF.


科目:初中数学 来源: 题型:
【题目】某校在“我运动,我快乐”的技能比赛培训活动中,在相同条件下,对甲、乙两名同学的“单手运球”项目进行了5次测试,测试成绩(单位:分)如下:根据右图判断正确的是( )

A.甲成绩的平均分低于乙成绩的平均分;
B.甲成绩的中位数高于乙成绩的中位数;
C.甲成绩的众数高于乙成绩的众数;
D.甲成绩的方差低于乙成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 的函数图象经过
的函数图象经过![]() 两点,过
两点,过![]() 两点作一直线.
两点作一直线.
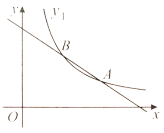
(1)求反比例函数解析式;
(2)将反比例函数![]() 向下平移1个单位,得函数
向下平移1个单位,得函数![]() ________;函数
________;函数![]() 与坐标轴的交点为__________;
与坐标轴的交点为__________;
(3)将直线![]() 向下平移
向下平移![]() 个单位后与函数
个单位后与函数![]() 的图象有唯一交点,求
的图象有唯一交点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2020个正方形的面积是____.
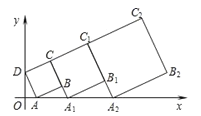
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
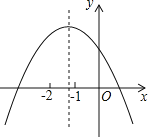
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
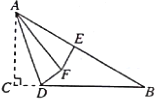
【题目】如图,已知在△ABC中,![]() ,
,![]() ,
,![]() ,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
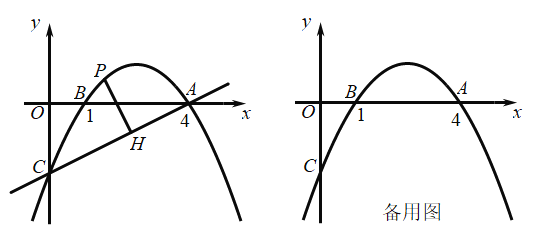
查看答案和解析>>
科目:初中数学 来源: 题型:
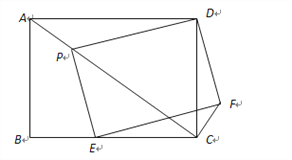
【题目】如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.
(1)若△PCD是等腰三角形时,求AP的长;
(2)若AP=![]() ,求CF的长.
,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
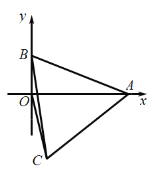
【题目】如图,在直角坐标系中,已知点A(6,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下作等边△ABC,连接OC,则OC的最小值( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com