
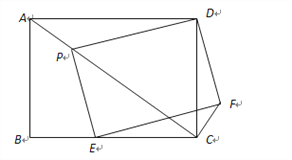
【题目】如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.
(1)若△PCD是等腰三角形时,求AP的长;
(2)若AP=![]() ,求CF的长.
,求CF的长.
【答案】(1)4;5;![]() (2)
(2)![]()
【解析】试题分析:(1)先求出AC,再分三种情况讨论计算即可得出结论;
(2)先判断出OC=![]() ED,OC=
ED,OC=![]() PF,进而得出OC=OP=OF,即可得出∠OCF=∠OFC,∠OCP=∠OPC,最后判断出△ADP∽△CDF,得出比例式即可得出结论.
PF,进而得出OC=OP=OF,即可得出∠OCF=∠OFC,∠OCP=∠OPC,最后判断出△ADP∽△CDF,得出比例式即可得出结论.
试题解析:(1)在矩形ABCD中,AB=6,AD=8,∠ADC=90°,∴DC=AB=6,
∴AC=![]() =10,
=10,
要使△PCD是等腰三角形,分三种情况讨论:
①当CP=CD时,AP=AC﹣CP=10﹣6=4;
②当PD=PC时,∠PDC=∠PCD,∵∠PCD+∠PAD=∠PDC+∠PDA=90°,∴∠PAD=∠PDA,∴PD=PA,∴PA=PC,∴AP=![]() AC=5;
AC=5;
③当DP=DC时,如图1,过点D作DQ⊥AC于Q,则PQ=CQ,∵S△ADC=![]() ADDC=
ADDC=![]() ACDQ,∴DQ=
ACDQ,∴DQ=![]() =
=![]() ,∴CQ=
,∴CQ=![]() =
=![]() ,∴PC=2CQ=
,∴PC=2CQ=![]() ,∴AP=AC﹣PC=10﹣
,∴AP=AC﹣PC=10﹣![]() =
=![]() ,
,
所以,若△PCD是等腰三角形时,AP=4或5或![]() ;
;
(2)如图2,连接PF,DE记PF与DE的交点为O,连接OC,
∵四边形ABCD和PEFD是矩形,∴∠ADC=∠PDF=90°,
∴∠ADP+∠PDC=∠PDC+∠CDF,∴∠ADP=∠CDF,
∠BCD=90°,OE=OD,∴OC=![]() ED,
ED,
在矩形PEFD中,PF=DE,∴OC=![]() PF,
PF,
∵OP=OF=![]() PF,∴OC=OP=OF,∴∠OCF=∠OFC,∠OCP=∠OPC,
PF,∴OC=OP=OF,∴∠OCF=∠OFC,∠OCP=∠OPC,
∵∠OPC+∠OFC+∠PCF=180°,∴2∠OCP+2∠OCF=180°,∴∠PCF=90°,
∴∠PCD+∠FCD=90°,
在Rt△ADC中,∠PCD+∠PAD=90°,∴∠PAD=∠FCD,
∴△ADP∽△CDF,∴![]() =
=![]() ,∵AP=
,∵AP=![]() ,∴CF=
,∴CF=![]() .
.


科目:初中数学 来源: 题型:
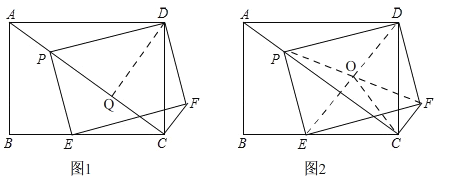
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
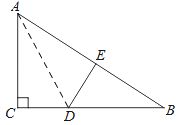
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
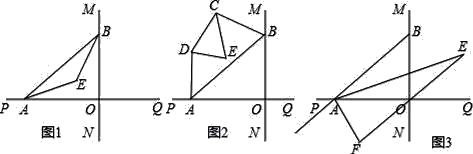
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(a,0),B(0,b),C(-a,0),且![]() +b2-4b+4=0.
+b2-4b+4=0.
(1)求证:∠ABC=90°;
(2)∠ABO的平分线交x轴于点D,求D点的坐标.
(3)如图,在线段AB上有两动点M、N满足∠MON=45°,求证:BM2+AN2=MN2.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P、Q分别为BC、CD边上一点,且BP=CQ=![]() BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=
BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=![]() ,则CE的长为_____.
,则CE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形ABCD,点E在线段AD上,将![]() 沿直线BE翻折后,点A落在线段CD上的点F.如果
沿直线BE翻折后,点A落在线段CD上的点F.如果![]() 的周长为12,
的周长为12,![]() 的周长为24,那么FC长为________.
的周长为24,那么FC长为________.
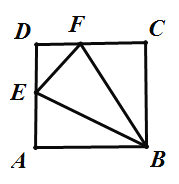
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的是带支架功能的某品牌手机壳,将其侧面抽象为如图2所示的几何图形,已知AB=5cm,∠BAC=60°,∠C=45°,则AC的长(![]() ≈1.732,结果精确到0.1cm)为( )
≈1.732,结果精确到0.1cm)为( )
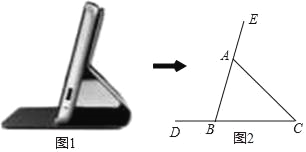
A. 3.4cm B. 4.6cm C. 5.8cm D. 6.8cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com