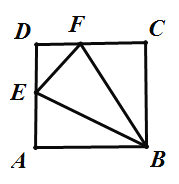
【题目】如图，已知长方形ABCD，点E在线段AD上，将
沿直线BE翻折后，点A落在线段CD上的点F.如果
的周长为12，
的周长为24，那么FC长为________.
【答案】6.
【解析】
由题意可得AE=EF，BF=AB=CD，根据△FDE的周长为12，△FCB的周长为24，可得DE+EF+DF=12，CF+BC+BF=24，等量代换后得CD+12- DF +CD-DF=24，于是可得（DC-DF）的值，即FC的长．
解：∵折叠后点A落在线段CD上的点F，
∴AE=EF，AB=BF，
∵四边形ABCD是长方形，
∴AD=BC，CD=AB，
∵△FDE的周长为12，△FCB的周长为24，
∴DE+EF+DF=12，BC+CF+FC=24，
∴DF+AD=12，AB+BC+CD-DF=24，
∴CD+12- DF +CD-DF=24，
∴CD-DF=6，
∴FC=6.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】七年级⑴班想买一些运动器材供班上同学阳光体育活动使用，班主任安排班长去商店买篮球和排球，下面是班长与售货员的对话：
班长：阿姨，您好！ 售货员：同学，你好，想买点什么？
⑴根据这段对话，你能算出篮球和排球的单价各是多少吗？
⑵六一儿童节店里搞活动有两种套餐，1、套装打折：五个篮球和五个排球为一套装，套装打 八折：2、满减活动：999 减 100，1999 减 200；两种活动不重复参与，学校需要 15个篮球，13 个排球作为奖品，请问如何安排购买更划算？
查看答案和解析>>
科目：初中数学 来源： 题型：
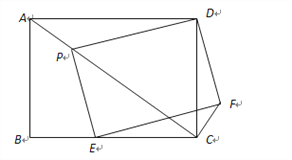
【题目】如图，矩形ABCD中，AB=6,AD=8，P,E分别是线段AC、BC上的点，且四边形PEFD为矩形．
（1）若△PCD是等腰三角形时，求AP的长；
（2）若AP=
，求CF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下图是2019年10月的月历，用如图所示的“凹”字型在月历中任意圈出5个数，设“凹”字型框中的五个数分别
，
，
，
，
.
（1）直接写出
______，
______（用含的式子表示）；
______；
（2）在移动“凹”字型框过程中，小明说被框住的5个数字之和可能为106，小敏说被框住的5个数字之和可能为90，你同意他们的说法吗？请说明理由；
（3）若另一个“凹”字型框框住的五个数分别为
，
，
，
，
，且
，则符合条件的的值为______.
查看答案和解析>>
科目：初中数学 来源： 题型：
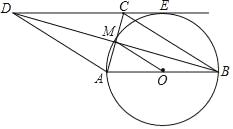
【题目】如图，四边形ABCD中，MA=MC，MB=MD，以AB为直径的O过点M且与DC延长线相切于点E．
（1）求证：四边形ABCD是菱形；
（2）若AB=4，求
的长（结果请保留π）
查看答案和解析>>
科目：初中数学 来源： 题型：
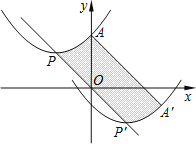
【题目】如图，抛物线的顶点为
，与y轴交于点
若平移该抛物线使其顶点P沿直线移动到点
，点A的对应点为
，则抛物线上PA段扫过的区域
阴影部分
的面积为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】两根木条，一根长20cm，另一根长24cm，将它们一端重合且放在同一条直线上，此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目：初中数学 来源： 题型：
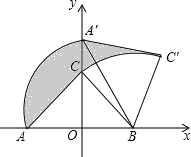
【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD内接于⊙O，A是弧BDC的中点，AE⊥AC于A，与⊙O及CB的延长线交于点F，E，且弧BF＝弧AD.
(1)求证：△ADC∽△EBA；
(2)如果AB＝8，CD＝5，求tan∠CAD的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com