
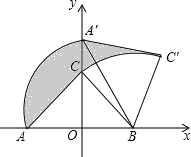
【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
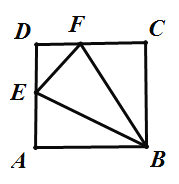
【题目】如图,已知长方形ABCD,点E在线段AD上,将![]() 沿直线BE翻折后,点A落在线段CD上的点F.如果
沿直线BE翻折后,点A落在线段CD上的点F.如果![]() 的周长为12,
的周长为12,![]() 的周长为24,那么FC长为________.
的周长为24,那么FC长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高斯上小学时,有一次数学老师让同学们计算“从1到100这100个正整数的和”.许多同学都采用了依次累加的计算方法,计算起来非常繁琐,且易出错.聪明的小高斯经过探索后,给出了下面漂亮的解答过程.
解:设S=1+2+3+…+100 ①
则S=100+99+98+…+1 ②
①+②,得(即左右两边分别相加):
2S=(1+100)+(2+99)+(3+98)+…+(100+1),
=![]() ,
,
=100×101,
所以,S=![]() ③,
③,
所以,1+2+3+…+100=5050.
后来人们将小高斯的这种解答方法概括为“倒序相加法”.请你利用“倒序相加法”解答下面的问题.
(1)计算:1+2+3+…+101;
(2)请你观察上面解答过程中的③式及你运算过程中出现的类似③式,猜想:1+2+3+…+n= ;
(3)至少用两种方法计算:1001+1002+…+2000.
方法1:
方法2:
查看答案和解析>>
科目:初中数学 来源: 题型:
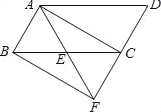
【题目】已知:如图,在ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,求证:四边形ABFC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=![]() 的图象与双曲线y=
的图象与双曲线y=![]() (k≠0,x>0)相交于点A(3,m)和点B.
(k≠0,x>0)相交于点A(3,m)和点B.
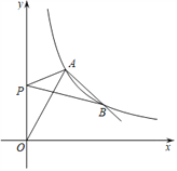
(1)求双曲线的解析式及点B的坐标;
(2)若点P在y轴上,连接PA,PB,求当PA+PB的值最小时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的是带支架功能的某品牌手机壳,将其侧面抽象为如图2所示的几何图形,已知AB=5cm,∠BAC=60°,∠C=45°,则AC的长(![]() ≈1.732,结果精确到0.1cm)为( )
≈1.732,结果精确到0.1cm)为( )
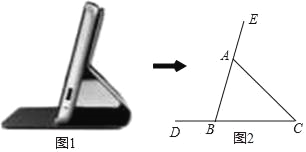
A. 3.4cm B. 4.6cm C. 5.8cm D. 6.8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
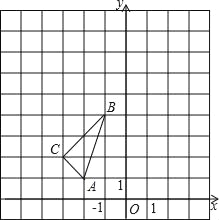
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF相交于点O,下列结论:
①∠DOC=90°,②OC=OE,③tan∠OCD=![]() ,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
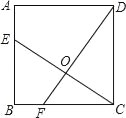
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com