
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
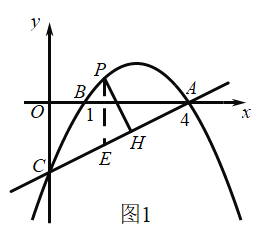
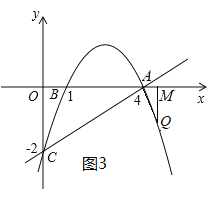
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
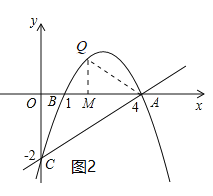
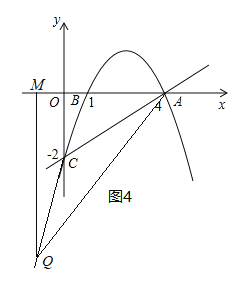
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
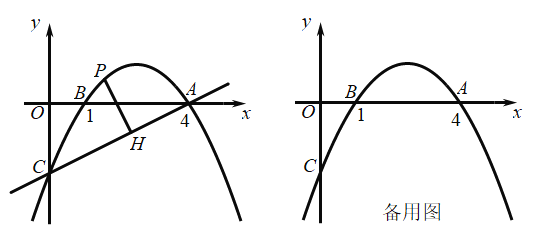
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)根据待定系数法解答即可;
(2)先利用待定系数法求出直线AC的解析式,过点 P 作 x 轴的垂线,交直线 AC 于点 E,如图1,设点P的横坐标为t,则PE可用含t的代数式表示,易证△PEH∽△ACO,可得![]() ,于是PH可用含t的代数式表示,然后根据二次函数的性质即可求出PH长度的最大值;
,于是PH可用含t的代数式表示,然后根据二次函数的性质即可求出PH长度的最大值;
(3)设Q点的横坐标为m,则Q点的纵坐标可用m的代数式表示,分三种情况:当1<m<4时,如图2;当m>4时,如图3;当m<1时,如图4,根据相似三角形的性质分![]() 与
与![]() 两种情况,建立关于m的方程求解即可.
两种情况,建立关于m的方程求解即可.
解:(1)将 A(4,0)、B(1,0)代入![]() ,
,
得:![]() ,解得
,解得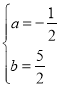 ,
,
∴抛物线的解析式为![]() ;
;
(2)将![]() 代入
代入![]() ,得
,得![]() ,∴
,∴![]() .
.
设直线 AC 的解析式为![]() ,
,
将 A(4,0)代入![]() ,解得:
,解得:![]() ,
,
∴直线 AC 的解析式为![]() .
.
过点 P 作 x 轴的垂线,交直线 AC 于点 E,如图1,
设 ![]() ,则
,则![]() .
.
∴![]() .
.
∵∠PEH=∠ACO,∠PHE=∠AOC=90°,
∴△PEH∽△ACO,
∴![]() ,
,
∴![]() .
.
∴当![]() 时,PH 有最大值
时,PH 有最大值![]() ;
;
(3)存在,点![]() 或
或![]() 或
或![]() .
.
理由如下:
设Q点的横坐标为m,则Q点的纵坐标为﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
当1<m<4时,如图2,AM=4﹣m,QM=﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
又∵∠COA=∠QMA=90°,
∴①当![]() 时,△AQM∽△ACO,即4﹣m=2(﹣
时,△AQM∽△ACO,即4﹣m=2(﹣![]() m2+
m2+![]() m﹣2),
m﹣2),
解得:m=2或m=4(舍去),
此时Q(2,1);
②当![]() 时,△AQM∽△CAO,即2(4﹣m)=﹣
时,△AQM∽△CAO,即2(4﹣m)=﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
解得:m=4或m=5(均不合题意,舍去);
当m>4时,如图3,AM=m-4,QM=![]() m2-
m2-![]() m+2,
m+2,
又∵∠COA=∠QMA=90°,
∴①当![]() 时,△AQM∽△ACO,即m-4=2(
时,△AQM∽△ACO,即m-4=2(![]() m2-
m2-![]() m+2),
m+2),
解得:m=2或m=4(均不合题意,舍去);
②当![]() 时,△AQM∽△CAO,即2(m-4)=
时,△AQM∽△CAO,即2(m-4)=![]() m2-
m2-![]() m+2,
m+2,
解得:m=5或m=4(不合题意,舍去);
∴Q(5,﹣2);
当m<1时,如图4,AM=4-m,QM=![]() m2-
m2-![]() m+2,
m+2,
又∵∠COA=∠QMA=90°,
①当![]() 时,△AQM∽△ACO,即4﹣m=2(
时,△AQM∽△ACO,即4﹣m=2(![]() m2-
m2-![]() m+2),
m+2),
解得:m=0或m=4(均不合题意,舍去);
②当![]() 时,△AQM∽△CAO,即2(4﹣m)=
时,△AQM∽△CAO,即2(4﹣m)=![]() m2-
m2-![]() m+2,
m+2,
解得:m=﹣3或m=4(不合题意,舍去);
∴Q(﹣3,﹣14);
综上所述,符合条件的点Q为(2,1)或(5,﹣2)或(﹣3,﹣14).


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图1是一把折叠椅子,图2是椅子完全打开支稳后的侧面示意图,![]() 表示地面所在的直线,其中
表示地面所在的直线,其中![]() 和
和![]() 表示两根较粗的钢管,
表示两根较粗的钢管,![]() 表示座板平面,
表示座板平面,![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,
,![]() 长
长![]() ,
,![]() ,
,![]() ,
,![]() 长
长![]() ,
,![]() 长
长![]() ,
,
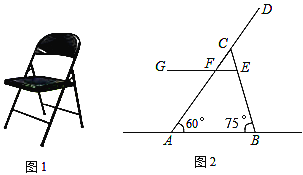
(1)求座板![]() 的长;
的长;
(2)求此时椅子的最大高度(即点![]() 到直线
到直线![]() 的距离).(结果保留根号)
的距离).(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
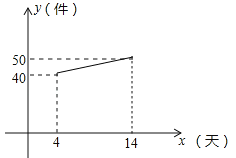
【题目】宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系: ![]() .
.
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AC=BC,CD是⊙O的直径,与AB相交于点G,过点D作EF∥AB,分别交CA、CB的延长线于点E、F,连接BD.
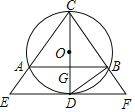
(1)求证:EF是⊙O的切线;
(2)求证:BD2=ACBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,![]() ,以BC为直径作
,以BC为直径作![]() 交AB于点E,D为AC边的中点,连接OD、DE,
交AB于点E,D为AC边的中点,连接OD、DE,
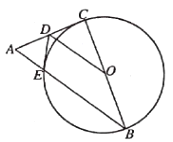
(1)求证:DE是![]() 的切线.
的切线.
(2)填空:①若![]() ,
,![]() ,则
,则![]() 的半径长是__________.
的半径长是__________.
②当∠A=__________时,四边形OCDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
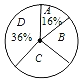
【题目】为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图(如图).请根据图表信息解答以下问题:
知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A | 60≤x<70 | a |
B | 70≤x<80 | 10 |
C | 80≤x<90 | 14 |
D | 90≤x≤100 | 18 |
(1)本次调查一共随机抽取了 名参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,AB:BC=2:1,且BE∥AC,CE∥DB,连接DE,则tan∠EDC=( )
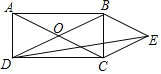
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm(如图1),点G为边BC(EF)的中点,边FD与AB相交于点H,此时线段BH的长是_____.现将三角板DEF绕点G按顺时针方向旋转(如图2),在∠CGF从0°到60°的变化过程中,点H相应移动的路径长共为_____.(结果保留根号)
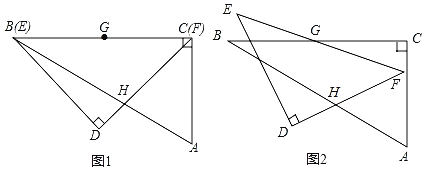
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com