
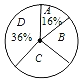
【题目】为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图(如图).请根据图表信息解答以下问题:
知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A | 60≤x<70 | a |
B | 70≤x<80 | 10 |
C | 80≤x<90 | 14 |
D | 90≤x≤100 | 18 |
(1)本次调查一共随机抽取了 名参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有 人.
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有三张卡片,分别标有数字1,2,3,这些卡片除数字不同外其余均相同.小明从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求第二次抽取卡片上的数字小于第一次抽取卡片上的数字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
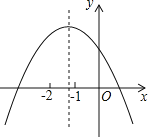
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
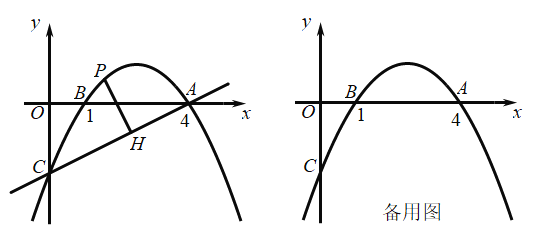
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新冠疫情防控期间,某医疗器械商业集团新进了40台A型电子体温测量仪,60台B型电子体温测量仪,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种测量仪每台的利润(元)如下表:
A型 | B型 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店![]() 台A型测量仪,集团卖出这100台测量仪的总利润为
台A型测量仪,集团卖出这100台测量仪的总利润为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围:
的取值范围:
(2)为了促销,集团决定仅对甲连锁店的A型测量仪每台让利![]() 元销售,其他的销售利润不变,并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润,问该集团应该如何设计调配方案,使总利润达到最大?
元销售,其他的销售利润不变,并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润,问该集团应该如何设计调配方案,使总利润达到最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
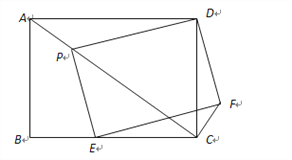
【题目】如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.
(1)若△PCD是等腰三角形时,求AP的长;
(2)若AP=![]() ,求CF的长.
,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
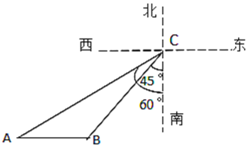
【题目】如图所示,在某海域,一艘指挥船在![]() 处收到渔船在
处收到渔船在![]() 处发出的求救信号,经确定,遇险抛锚的渔船所在的
处发出的求救信号,经确定,遇险抛锚的渔船所在的![]() 处位于
处位于![]() 处的南偏西45°方向上,且
处的南偏西45°方向上,且![]() 海里;指挥船搜索发现,在
海里;指挥船搜索发现,在![]() 处的南偏西60°方向上有一艘海监船
处的南偏西60°方向上有一艘海监船![]() ,恰好位于
,恰好位于![]() 处的正西方向.于是命令海监船
处的正西方向.于是命令海监船![]() 前往搜救,已知海监船
前往搜救,已知海监船![]() 的航行速度为30海里/小时,问渔船在
的航行速度为30海里/小时,问渔船在![]() 处需要等待多长时间才能得到海监船
处需要等待多长时间才能得到海监船![]() 的救援?(参考数据:
的救援?(参考数据:![]() 、
、![]() 、
、![]() 结果精确到0.1小时)
结果精确到0.1小时)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三位同学到小新家做客,小新用如图所示的一次性茶杯给三位同学分别倒了一杯开水,三个杯子从外观看无任何区别,若三位同学均喝完杯中水后外出玩耍,回来后对水杯放置的位置均已忘记.

(1)现A同学随手从三个已用杯子中拿一个杯子,“拿到自己已用杯子”这一事件是________事件,“拿到大家都没用过的杯子”这一事件是__________事件;
(2)A同学先取一个杯子,B同学在剩下的两个杯子中取一个杯子,求两同学均恰好拿到自己已用杯子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
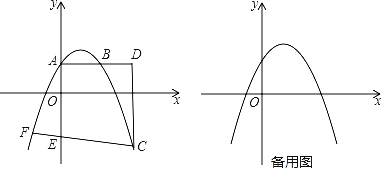
【题目】如图所示,抛物线y=ax2+bx+4的顶点坐标为(3,![]() ),与y轴交于点A.过点A作AB∥x轴,交抛物线于点B,点C是第四象限的抛物线上的一个动点,过点C作y轴的平行线,交直线AB于点D.
),与y轴交于点A.过点A作AB∥x轴,交抛物线于点B,点C是第四象限的抛物线上的一个动点,过点C作y轴的平行线,交直线AB于点D.
(1)求抛物线的函数表达式;
(2)若点E在y轴的负半轴上,且AE=AD,直线CE交抛物线y=ax2+bx+4于点F.
①求点F的坐标;
②过点D作DG⊥CE于点G,连接OD、ED,当∠ODE=∠CDG时,求直线DG的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com