
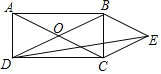
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,AB:BC=2:1,且BE∥AC,CE∥DB,连接DE,则tan∠EDC=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 的函数图象经过
的函数图象经过![]() 两点,过
两点,过![]() 两点作一直线.
两点作一直线.
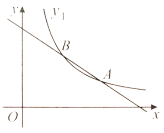
(1)求反比例函数解析式;
(2)将反比例函数![]() 向下平移1个单位,得函数
向下平移1个单位,得函数![]() ________;函数
________;函数![]() 与坐标轴的交点为__________;
与坐标轴的交点为__________;
(3)将直线![]() 向下平移
向下平移![]() 个单位后与函数
个单位后与函数![]() 的图象有唯一交点,求
的图象有唯一交点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
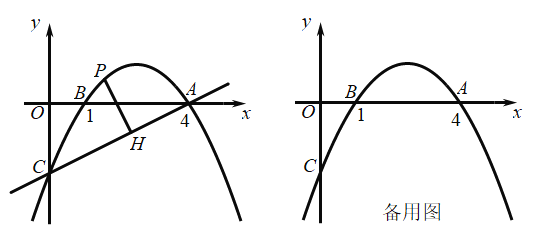
查看答案和解析>>
科目:初中数学 来源: 题型:
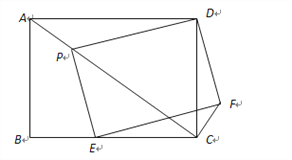
【题目】如图,矩形ABCD中,AB=6,AD=8,P,E分别是线段AC、BC上的点,且四边形PEFD为矩形.
(1)若△PCD是等腰三角形时,求AP的长;
(2)若AP=![]() ,求CF的长.
,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
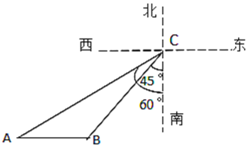
【题目】如图所示,在某海域,一艘指挥船在![]() 处收到渔船在
处收到渔船在![]() 处发出的求救信号,经确定,遇险抛锚的渔船所在的
处发出的求救信号,经确定,遇险抛锚的渔船所在的![]() 处位于
处位于![]() 处的南偏西45°方向上,且
处的南偏西45°方向上,且![]() 海里;指挥船搜索发现,在
海里;指挥船搜索发现,在![]() 处的南偏西60°方向上有一艘海监船
处的南偏西60°方向上有一艘海监船![]() ,恰好位于
,恰好位于![]() 处的正西方向.于是命令海监船
处的正西方向.于是命令海监船![]() 前往搜救,已知海监船
前往搜救,已知海监船![]() 的航行速度为30海里/小时,问渔船在
的航行速度为30海里/小时,问渔船在![]() 处需要等待多长时间才能得到海监船
处需要等待多长时间才能得到海监船![]() 的救援?(参考数据:
的救援?(参考数据:![]() 、
、![]() 、
、![]() 结果精确到0.1小时)
结果精确到0.1小时)
查看答案和解析>>
科目:初中数学 来源: 题型:
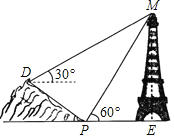
【题目】小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=![]() ,请你帮助小明计算古塔的高度ME.(结果保留根号)
,请你帮助小明计算古塔的高度ME.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三位同学到小新家做客,小新用如图所示的一次性茶杯给三位同学分别倒了一杯开水,三个杯子从外观看无任何区别,若三位同学均喝完杯中水后外出玩耍,回来后对水杯放置的位置均已忘记.

(1)现A同学随手从三个已用杯子中拿一个杯子,“拿到自己已用杯子”这一事件是________事件,“拿到大家都没用过的杯子”这一事件是__________事件;
(2)A同学先取一个杯子,B同学在剩下的两个杯子中取一个杯子,求两同学均恰好拿到自己已用杯子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
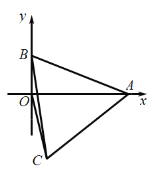
【题目】如图,在直角坐标系中,已知点A(6,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下作等边△ABC,连接OC,则OC的最小值( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com