练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．已知a、b、m是实数，4a2-4am+m2+|m-2b|+$\sqrt{b-2}=0$，求（ab）m的值．

    分析 原式即（2a-m）2+|m-2b|+$\sqrt{b-2}$=0，根据非负数的性质即可得到关于a、b、m的方程组，求得a、b、m的值，然后代入求值．

    解答 解：原式即：（2a-m）2+|m-2b|+$\sqrt{b-2}$=0，
    则$\left\{\begin{array}{l}{2a-m=0}\\{m-2b=0}\\{b-2=0}\end{array}\right.$，
    解得：$\left\{\begin{array}{l}{a=2}\\{b=2}\\{m=4}\end{array}\right.$，
    则原式=（2×2）4=44=256．

    点评 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

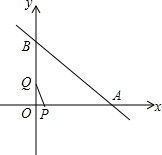    8．如图，直线y=-x+8与x轴、y轴交于A、B两点，点P、点Q同时从点O出发，分别以每秒3个单位和每秒4个单位的速度沿x轴、y轴方向移动，连接PQ．设移动的时间为t秒（0＜t＜2），以点P为中心，顺时针旋转△POQ，使旋转后的△O′PQ′的边PQ′恰好落在x轴上．
    （1）当点Q′与点A重合时，求此时的t的值；
    （2）设△O′PQ′与△ABO重叠部分的面积为S，求S与t的函数关系式，并直接写出t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图所示，三角形ABC是通过平移三角形DEF得到的，已知ED和BA是对应线段，请在图中画出三角形DEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

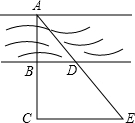    6．如图，为了测量河宽，小华采用的办法是：在河的对岸选取一点A，在河的这岸选一点B，使AB与河的边缘垂直，然后在AB的延长线上取一点C，并量得BC=30米；在河的这边取一点D，并量得BD=20米；最后在射线AD上取一点E，使得CE∥BD，并量得DE=40米．小华这种做法，她能根据已有的数据求出河宽AB吗？若能，请求出河宽AB；若不能，她还必须测量哪一条线段的长？假设这条线段的长是m米，请你用含m的代数式表示河宽AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

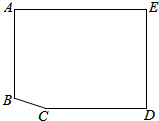    2．有一山庄，它的平面图为如图③的五边形ABCDE，山庄保卫人员想在线段CD上选一点M安装监控装置，用来监视边AB，现只要使∠AMB大约为60°，就可以让监控装置的效果达到最佳，已知∠A=∠E=∠D=90°，AB=270m，AE=400m，ED=285m，CD=340m，问在线段CD上是否存在点M，使∠AMB=60°？若存在，请求出符合条件的DM的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．画一条数轴，在数轴上表示下列各数以及它们的相反数，并用“＜”将这四个数连接起来．
    -1.5，-4，2$\frac{1}{2}$，-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．-32-[-5+（1-0.2÷$\frac{3}{5}$）÷（-3）2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：
    （1）-32+23+4×|-5|；
    （2）（$\frac{2}{3}$-$\frac{3}{4}$+$\frac{5}{6}$）÷$\frac{1}{12}$+（-22×$\frac{1}{2}$）-（-2）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．已知线段AB延长线段AB到C，使BC=2AB，反向延长AB到D，使AD=AB，则AC=3AB；DC=$\frac{4}{3}$AC．

    查看答案和解析>>

    同步练习册答案