
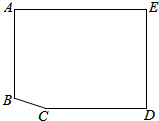
 有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳,已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长;若不存在,请说明理由.
有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳,已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长;若不存在,请说明理由. 分析 要满足∠AMB=60°,可构造以AB为边的等边三角形的外接圆,该圆与线段CD的交点就是满足条件的点,然后借助于等边三角形的性质、特殊角的三角函数值等知识,就可算出符合条件的DM长.
解答 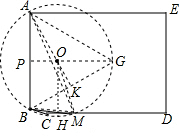 解:在线段CD上存在点M,使∠AMB=60°.
解:在线段CD上存在点M,使∠AMB=60°.
理由如下:
以AB为边,在AB的右侧作等边三角形ABG,
作GP⊥AB,垂足为P,作AK⊥BG,垂足为K.
设GP与AK交于点O,以点O为圆心,OA为半径作⊙O,
过点O作OH⊥CD,垂足为H,如图.
则⊙O是△ABG的外接圆,
∵△ABG是等边三角形,GP⊥AB,
∴AP=PB=$\frac{1}{2}$AB.
∵AB=270,
∴AP=135.
∵ED=285,
∴OH=285-135=150.
∵△ABG是等边三角形,AK⊥BG,
∴∠BAK=∠GAK=30°.
∴OP=AP•tan30°,
=135×$\frac{\sqrt{3}}{3}$=45$\sqrt{3}$.
∴OA=2OP=90$\sqrt{3}$.
∴OH<OA.
∴⊙O与CD相交,设交点为M,连接MA、MB,
∴∠AMB=∠AGB=60°,OM=OA=90$\sqrt{3}$.
∵OH⊥CD,OH=150,OM=90$\sqrt{3}$,
∴HM=$\sqrt{{OM}^{2}-{OH}^{2}}$=$\sqrt{(90\sqrt{3})^{2}-{150}^{2}}$=30$\sqrt{3}$.
∵AE=400,OP=45$\sqrt{3}$,
∴DH=400-45$\sqrt{3}$.
若点M在点H的左边,则DM=DH+HM=400-45$\sqrt{3}$+30$\sqrt{2}$.
∵400-45$\sqrt{3}$+30$\sqrt{2}$>340,
∴DM>CD.
∴点M不在线段CD上,应舍去.
若点M在点H的右边,则DM=DH-HM=400-45$\sqrt{3}$-30$\sqrt{2}$.
∵400-45$\sqrt{3}$-30$\sqrt{2}$<340,
∴DM<CD.
∴点M在线段CD上.
综上所述:在线段CD上存在唯一的点M,使∠AMB=60°,
此时DM的长为(400-45$\sqrt{3}$-30$\sqrt{2}$)米.
点评 本题考查了圆综合题,涉及垂直平分线的性质、矩形的性质、等边三角形的性质、直线与圆的位置关系、圆周角定理、勾股定理等知识,考查了操作、探究等能力,综合性非常强.而构造等边三角形及其外接圆是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
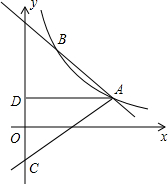 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com