
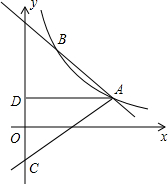
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.分析 (1)根据反比例函数图象上点的坐标特征易得k=2$\sqrt{3}$,从而求得反比例函数解析式;
(2)作BH⊥AD于H,如图1,根据反比例函数图象上点的坐标特征确定B点坐标为(1,2$\sqrt{3}$),确定AH=2$\sqrt{3}$-1,BH=2$\sqrt{3}$-1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC-∠BAH=30°,根据特殊角的三角函数值得tan∠DAC=$\frac{\sqrt{3}}{3}$;由于AD⊥y轴,则OD=1,AD=2$\sqrt{3}$,然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,-1),于是可根据待定系数法求出直线AC的解析式为y=$\frac{\sqrt{3}}{3}$x-1;
解答 解:(1)由反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),得:
k=2$\sqrt{3}$×1=2$\sqrt{3}$,
∴反比例函数为y=$\frac{2\sqrt{3}}{x}$(x>0),
(2)作BH⊥AD于H,如图1,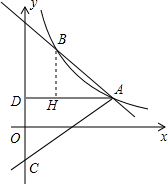
把B(1,a)代入反比例函数解析式y=$\frac{2\sqrt{3}}{x}$(x>0),得a=2$\sqrt{3}$,
∴B点坐标为(1,2$\sqrt{3}$),
∴AH=2$\sqrt{3}$-1,BH=2$\sqrt{3}$-1,
∴△ABH为等腰直角三角形,
∴∠BAH=45°,
∵∠BAC=75°,
∴∠DAC=∠BAC-∠BAH=30°,
∴tan∠DAC=tan30°=$\frac{\sqrt{3}}{3}$;
∵AD⊥y轴,
∴OD=1,AD=2$\sqrt{3}$,
∵tan∠DAC=$\frac{CD}{DA}$=$\frac{\sqrt{3}}{3}$,
∴CD=2,
∴OC=1,
∴C点坐标为(0,-1),
设直线AC的解析式为y=kx+b,
把A(2$\sqrt{3}$,1)、C(0,-1)代入
得$\left\{\begin{array}{l}{2\sqrt{3}k+b=1}\\{b=-1}\end{array}\right.$,
解$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-1}\end{array}\right.$,
∴直线AC的解析式为y=$\frac{\sqrt{3}}{3}$x-1;
点评 本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和待定系数法求一次函数解析式;作出辅助线构建直角三角形是解题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
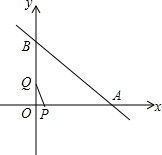 如图,直线y=-x+8与x轴、y轴交于A、B两点,点P、点Q同时从点O出发,分别以每秒3个单位和每秒4个单位的速度沿x轴、y轴方向移动,连接PQ.设移动的时间为t秒(0<t<2),以点P为中心,顺时针旋转△POQ,使旋转后的△O′PQ′的边PQ′恰好落在x轴上.
如图,直线y=-x+8与x轴、y轴交于A、B两点,点P、点Q同时从点O出发,分别以每秒3个单位和每秒4个单位的速度沿x轴、y轴方向移动,连接PQ.设移动的时间为t秒(0<t<2),以点P为中心,顺时针旋转△POQ,使旋转后的△O′PQ′的边PQ′恰好落在x轴上. 查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
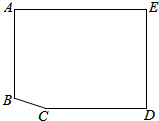 有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳,已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长;若不存在,请说明理由.
有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳,已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com