
分析 (1)由已知的等式得出$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)利用上面的规律拆分相互抵消计算即可.
解答 解:(1)$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2012×2013}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2012}$-$\frac{1}{2013}$
=1-$\frac{1}{2013}$
=$\frac{2012}{2013}$.
点评 此题考查有理数的混合运算,利用拆分的规律,拆分计算,相互抵消是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
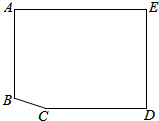 有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳,已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长;若不存在,请说明理由.
有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳,已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com