
��Rt��ABC�У���ACB=90�㣬��A=30�㣬BD�ǡ�ABC�Ľ�ƽ���ߣ� DE��AB�ڵ�E��
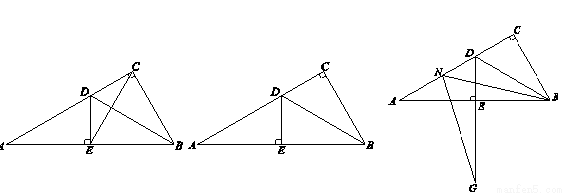
��1����ͼ1������EC����֤����EBC�ǵȱ������Σ�
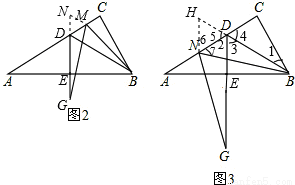
��2����M���߶�CD�ϵ�һ�㣨�����C��D�غϣ�����BMΪһ�ߣ���BM���·�����BMG=60�㣬MG��DE�ӳ����ڵ�G��������ͼ2�л�������ͼ�Σ���ֱ��д��MD��DG��AD֮���������ϵ��
��3����ͼ3,��N���߶�AD�ϵ�һ�㣬��BNΪһ�ߣ���BN���·�����BNG=60�㣬NG��DE�ӳ����ڵ�G����̽��ND��DG��AD����֮��Ĺ�ϵ����˵�����ɣ�
��1��֤������������2��AD=DG+DM����3��AD=DG-DN�����ɼ�����.
��������
�����������1�����á�������ȡ����������ǵȱ�������֤�á�EBC�ǵȱ������Σ�
��2���ӳ�EDʹ��DN=DM������MN�����ɵó���NDM�ǵȱ������Σ����á�NGM�ա�DBM���ɵó�BD=NG=DG+DM��������AD=BD�����ɵó��𰸣�
��3�����õȱ������ε����ʵó���H=��2�������ó���DNG=��HNB���������DNG�ա�HNB���ɵó��𰸣�
�����������1��֤������ͼ1��ʾ��
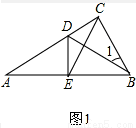
��Rt��ABC�У���ACB=90�㣬��A=30�㣬
���ABC=60�㣬BC=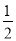 AB��
AB��
��BDƽ�֡�ABC��
���1=��DBA=��A=30�㣮
��DA=DB��
��DE��AB�ڵ�E��
��AE=BE=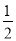 AB��
AB��
��BC=BE��
���EBC�ǵȱ������Σ�
��2�����ۣ�AD=DG+DM��
֤������ͼ2��ʾ���ӳ�EDʹ��DN=DM������MN��
�ߡ�ACB=90�㣬��A=30�㣬BD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AB�ڵ�E��
���ADE=��BDE=60�㣬AD=BD��
�֡�DM=DN��
���NDM�ǵȱ������Σ�
��MN=DM��
�ڡ�NGM�͡�DBM�У�
��
���NGM�ա�DBM��
��BD=NG=DG+DM��
��AD=DG+DM��
��3�����ۣ�AD=DG-DN��
֤�����ӳ�BD��H��ʹ��DH=DN��
�ɣ�1����DA=DB����A=30�㣮
��DE��AB�ڵ�E��
���2=��3=60�㣮
���4=��5=60�㣮
���NDH�ǵȱ������Σ�
��NH=ND����H=��6=60�㣮
���H=��2��
�ߡ�BNG=60�㣬
���BNG+��7=��6+��7��
����DNG=��HNB��
�ڡ�DNG�͡�HNB�У�

���DNG�ա�HNB��ASA����
��DG=HB��
��HB=HD+DB=ND+AD��
��DG=ND+AD��
��AD=DG-ND��
���㣺1.�ȱ������ε��ж������ʣ�2.ȫ�������ε��ж������ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
�����������ѧ��쳲��������о����ӷ�ֳ����ʱ������������һ������1��1��2��3��5��8��13���������дӵ���������ÿһ������������ǰ���������ĺͣ������������еĸ�������Ϊ�����εı߳�ֵ���������Σ��ٷֱ����δ�����ȡ2����3����4����5����������ƴ�����ϳ����Σ������˹��ɼ����������Σ������Ϊ�ߵij������ܳ��� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ�Ͼ���������Ƭ���꼶��ѧ�����м����ѧ�Ծ��������棩 ���ͣ�ѡ����
���и������У������ȵ��ǣ� ��
A�� ��
��
B�� ��
��
C�� ��
��
D�� ��
�� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶12���¿���ѧ�Ծ��������棩 ���ͣ������
һ�κ���y=��2x+1��ͼ������ ���ޡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶12���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
��A��-3��-4����ԭ��ľ���Ϊ�� ��
��A��3 ��B��4 ��C��5 ��D��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱���а��꼶��ѧ�����м����ѧ�Ծ��������棩 ���ͣ������
��֪����ͼ��A��B��C��D�ĵ���ͬһֱ���ϣ� AB=CD��AE��BF��AE=BF����֤��EC=FD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�걱���а��꼶��ѧ�����м����ѧ�Ծ��������棩 ���ͣ������
��ͼ����ABC�ǵ���ֱ�������Σ���C=90�㣬BDƽ�֡�CBA��AC�ڵ�D��DE��AB��E������ADB�����Ϊ6��CD =2����AB= ��
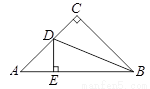
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ���Ĵ�ʡ����������ѧУ���꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��֪���� �ķ���
�ķ��� ��
��
��֤����1������mΪ��ֵ�������ǹ��� ��һԪ���η��̡�
��һԪ���η��̡�
��2������mΪ��ֵ������������������ȵ�ʵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶��ѧ�ڵڶ����¿���ѧ�Ծ��������棩 ���ͣ������
һ������ֱ����80cm��ĸ�߳�Ϊ90cm��Բ�IJ���չ��ͼ��Բ�ĽǵĶ���Ϊ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com