
【题目】已知:在梯形ABCD中,AD//BC,AC=BC=10,![]() ,点E在对角线AC上,且CE=AD,BE的延长线与射线AD、射线CD分别相交于点F、G.设AD=x,△AEF的面积为y.
,点E在对角线AC上,且CE=AD,BE的延长线与射线AD、射线CD分别相交于点F、G.设AD=x,△AEF的面积为y.
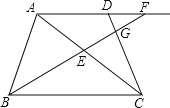
(1)求证:∠DCA=∠EBC;
(2)如图,当点G在线段CD上时,求y关于x的函数解析式,并写出它的定义域;
(3)如果△DFG是直角三角形,求△AEF的面积.
【答案】(1)见解析;(2)![]() ,
,![]() ;(3)15或
;(3)15或![]() .
.
【解析】
(1)由AD与BC平行,得到一对内错角相等,再由AD=CE,AC=BC,利用SAS可得△DCA≌△ECB,由全等三角形的性质可得结论;
(2)由AD与BC平行,得到三角形AEF与三角形CEB相似,由相似得比例表示出AF,过E作EH垂直于AF,根据锐角三角函数定义表示出EH,进而表示出y与x的函数解析式,并求出x的范围即可;
(3)分两种情况考虑:①当∠FDG=90°时,如图2所示,在直角三角形ACD中,利用锐角三角函数定义求出AD的长,即为x的值,代入求出y的值,即为三角形AEF面积;②当∠DGF=90°时,过E作EM⊥BC于点M,如图3所示,由相似列出关于x的方程,求出方程的解得到x的值,进而求出y的值,即为三角形AEF面积.
解:(1)证明:∵AD∥BC,
∴∠DAC=∠ECB,
在△DCA和△ECB中,
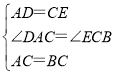 ,
,
∴△DCA≌△ECB(SAS),
∴∠DCA=∠EBC;
(2)∵AD∥BC,
∴△AEF∽△CEB,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
作EH⊥AF于H,如图1所示,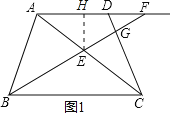
![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∵点G在线段CD上,
∴AF≥AD,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴y关于x的函数解析式为:![]() ,定义域为
,定义域为![]() .
.
(3)(3)分两种情况考虑:
①当∠FDG=90°时,如图2所示:
在Rt△ADC中,![]() ,即
,即![]() ,
,
∴![]() ;
;
②当∠DGF=90°时,过E作EM⊥BC于点M,如图3所示,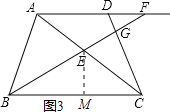
由(1)得:CE=AD=x,
在Rt△EMC中,![]() ,
,![]() ,
,
∴![]() ,
,
∵∠GCE=∠GBC,∠EGC=∠CGB,
∴△CGE∽△BGC,
∴![]() ,即
,即![]() ,
,
∵∠EBM=∠CBG,∠BME=∠BGC=90°,
∴△BME∽△BGC,
∴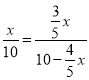 ,即
,即![]() ,
,
此时![]() ,
,
∴综上,此时△AEF的面积为![]() 或15.
或15.


科目:初中数学 来源: 题型:
【题目】秋风送爽,学校组织同学们去颐和园秋游,昆明湖西堤六桥中的玉带桥最是令人喜爱,如图所示,玉带桥的桥拱是抛物线形水面宽度AB=10m,桥拱最高点C到水面的距离为6m.
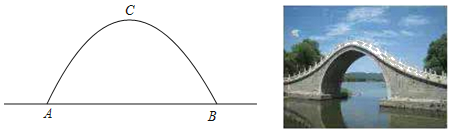
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一艘游船高度是4.5m,宽度是4m,为了保证安全,船顶距离桥拱顶部至少0.5m,通过计算说明这艘游船能否安全通过玉带桥.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点 M 满足横、纵坐标都为整数,则把点 M 叫做“整点”.例如:P(1,0)、Q(2,-2)都是“整点”.抛物线 y=mx2-2mx+m-1(m>0)与 x 轴交于 A、 B 两点,若该抛物线在 A、B 之间的部分与线段 AB 所围成的区域(包括边界)恰有 6 个整点,则 m 的取值范围是( )
A.![]() m
m ![]() B.
B.![]() m
m ![]() C.
C.![]() m
m ![]() D.
D.![]() m
m ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于(-1,0)点,则下列结论中正确的是( )

A.c<0B.a-b+c<0C.b2<4acD.2a+b=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4 经过点A(﹣3,0),点 B 在抛物线上,CB∥x轴,且AB 平分∠CAO.则此抛物线的解析式是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 个边长为
个边长为![]() 的相邻正方形的一边均在同一直线上,点
的相邻正方形的一边均在同一直线上,点![]() ,
,![]() ,
,![]() ,…
,…![]() 分别为边
分别为边![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的中点,
的中点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,…
,…![]() 的面积为
的面积为![]() ,则
,则![]() ________.(用含
________.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
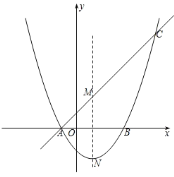
(1)求抛物线的函数关系式;
(2)设题中的抛物线与直线的另一交点为C,已知P(x,y)为线段AC上一点,过点P作PQ⊥x轴,交抛物线于点Q.求线段PQ的最大值及此时P坐标;
(3)在(2)的条件下,求△AQC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x-3,下列说法中正确的是( )
A.该函数图象的开口向下B.该函数图象的顶点坐标是(-2,-7)
C.当x<0时,y随x的增大而增大D.该函数图象与x轴有两个不同的交点,且分布在坐标原点两侧
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com