
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于(-1,0)点,则下列结论中正确的是( )

A.c<0B.a-b+c<0C.b2<4acD.2a+b=0
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出△ABC关于原点成中心对称的三角形△A′B′C′;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点B″的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边 AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).

(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物
线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段
AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在梯形ABCD中,AD//BC,AC=BC=10,![]() ,点E在对角线AC上,且CE=AD,BE的延长线与射线AD、射线CD分别相交于点F、G.设AD=x,△AEF的面积为y.
,点E在对角线AC上,且CE=AD,BE的延长线与射线AD、射线CD分别相交于点F、G.设AD=x,△AEF的面积为y.
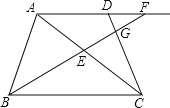
(1)求证:∠DCA=∠EBC;
(2)如图,当点G在线段CD上时,求y关于x的函数解析式,并写出它的定义域;
(3)如果△DFG是直角三角形,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,D,E在△ABC的边BC上,若△ADE是等边三角形则称△ABC可内嵌,△ADE叫做△ABC的内嵌三角形.

(1)直角三角形______可内嵌.(填写“一定”、“一定不”或“不一定”)
(2)如图2,在△ABC中,∠BAC=120°,△ADE是△ABC的内嵌三角形,试说明AB2=BDBC是否成立?如果成立,请给出证明;如果不一定成立,请举例说明.
(3)在(2)的条件下,如果AB=1,AC=2,求△ABC的内嵌△ADE的边长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形纸片ABC,面积为25,BC的长为10,∠B、∠C都为锐角,M为AB边上的一动点(M与A、B不重合),过点M作MN∥BC交AC于点N,设MN=x.
(1)用x表示△AMN的面积;
(2)△AMN沿MN折叠,使△AMN紧贴四边形BCNM(边AM、AN落在四边形BCNM所在的平面内),设点A落在平面BCNM内的点A′,△A′MN与四边形BCNM重叠部分的面积为y.
①用含x的代数式表示y,并写出x的取值范围.
②当x为何值时,重叠部分的面积y最大,最大为多少?
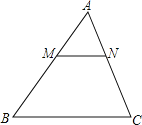
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com