
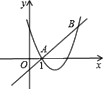
【题目】如图,直线![]() 和抛物线
和抛物线![]() 都经过点A(1,0),B,且当
都经过点A(1,0),B,且当![]() 时,二次函数的值为
时,二次函数的值为![]() .
.
(1)求![]() 的值和抛物线的解析式;
的值和抛物线的解析式;
(2)求不等式![]() 的解集.
的解集.
【答案】(1)m=1;y=x23x+2;(2)x<1或x>3.
【解析】
(1)直接把点A(1,0)代入直线y=x+m即可得出m的值;再把点A(1,0)与当x=4时,y=6代入抛物线y=x2+bx+c即可得出b、c的值,进而得出抛物线的解析式;
(2)根据(1)中m、b、c的值即可得出一次函数与二次函数的解析式,故可得出B点坐标,根据函数的图象即可得出结论.
(1)∵直线y=x+m和经过点A(1,0),
∴1+m=0,解得m=1;
∵抛物线y=x2+bx+c经过点A(1,0),且当x=4时,二次函数的值为6,
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为y=x23x+2;
(2)∵由(1)知m=1,抛物线的解析式为y=x23x+2,
∴直线的解析式为y=x1,
∴![]() ,解得
,解得![]() 或
或![]() ,
,
∴B(3,2).
∵由函数图象可知,当x<1或x>3时,二次函数的值大于一次函数的值,
∴不等式x2+bx+c>x+m的解集为x<1或x>3.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
①ac>0;②16a+4b+c=0;③若m>n>0,则x=1+m时的函数值大于x=1﹣n时的函数值;④点(﹣![]() ,0)一定在此抛物线上.其中正确结论的序号是( )
,0)一定在此抛物线上.其中正确结论的序号是( )
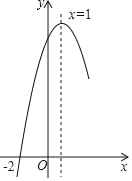
A. ①②B. ②③C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
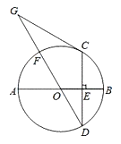
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
(1)求证:CG是⊙O的切线 (2)若CD=6,求GF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )

A、3.25m B、4.25m C、4.45m D、4.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于(-1,0)点,则下列结论中正确的是( )

A.c<0B.a-b+c<0C.b2<4acD.2a+b=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC形内一点,且∠APB=∠APC=135°.
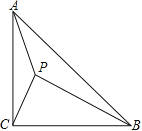
(1)求证:△CPA∽△APB;
(2)试求tan∠PCB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4 经过点A(﹣3,0),点 B 在抛物线上,CB∥x轴,且AB 平分∠CAO.则此抛物线的解析式是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l:
中,直线l:![]() 与直线
与直线![]() ,直线
,直线![]() 分别交于点A,B,直线
分别交于点A,B,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,结合函数图象,求区域
时,结合函数图象,求区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内没有整点,直接写出
内没有整点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com