
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC形内一点,且∠APB=∠APC=135°.
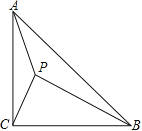
(1)求证:△CPA∽△APB;
(2)试求tan∠PCB的值.
【答案】(1)见解析 (2)2.
【解析】
试题(1)根据∠PBA+∠PAB=45°和∠PAC+∠PAB=45°得出∠PAC=∠PBA,再根据已知条件∠APB=∠APC得出三角形相似;(2)根据等腰直角三角形的性质得出CA和AB的比值,设CP=k,则PB=2k,然后根据∠BPC=90°求出∠PCB的正切值.
试题解析:(1)∵在△ABC中,∠ACB=90°,AC=BC,∴∠BAC=45°,即∠PAC+∠PAB=45°,
又在△APB中,∠APB=135°, ∴∠PBA+∠PAB=45°, ∴∠PAC=∠PBA,
又∠APB=∠APC, ∴△CPA∽△APB.
(2)∵△ABC是等腰直角三角形,
∴![]() , 又∵△CPA∽△APB, ∴
, 又∵△CPA∽△APB, ∴![]() ,
,
令CP=k,则![]() ,
,
又在△BCP中,∠BPC=360°﹣∠APC﹣∠APB=90°, ∴![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>![]() 时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
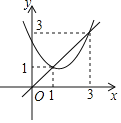
A. ①②④B. ②③④C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以2cm/s的速度向点A匀速运动,同时动点N从点C出发,在CB边上以![]() cm/s的速度向点B匀速运动,设运动时间为ts(0≤t≤5),连接MN.
cm/s的速度向点B匀速运动,设运动时间为ts(0≤t≤5),连接MN.

发现:BM= cm,BN= cm;(用含t的式子来表示)
猜想:(1)若BM=BN,求t值;
(2)若△MBN与△ABC相似,求t值.
探究:是否存在符合条件的t,使△BMN与四边形AMNC面积相等?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。

(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=mx2+2mx﹣3与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,且x2﹣x1=4.
(1)求抛物线的解析式;
(2)求抛物线的对称轴上存在一点P,使PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标.
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.
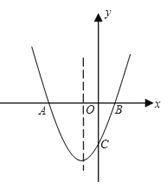
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=12,AD平分∠BAC,交BC于点 E,交⊙O于点D,连接BD.

(1)求证:∠BAD=∠CBD;
(2)若∠AEB=125°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a![]() 0)的图象过点(-2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;④若方程a(x+2)(4-x)=-2的两根为x1,x2,且x1<x2,则-2
0)的图象过点(-2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;④若方程a(x+2)(4-x)=-2的两根为x1,x2,且x1<x2,则-2![]() x1<x2<4.
x1<x2<4.
其中结论正确的有( )
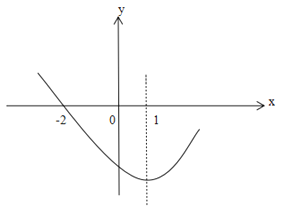
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com