
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.

【答案】4
【解析】
由![]() ,
,![]() 和
和![]() 坐标都满足函数
坐标都满足函数![]() ,∴①是正确的;从图象可以看出图象具有对称性,对称轴可用对称轴公式求得是直线
,∴①是正确的;从图象可以看出图象具有对称性,对称轴可用对称轴公式求得是直线![]() ,②也是正确的;
,②也是正确的;
根据函数的图象和性质,发现当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大,因此③也是正确的;函数图象的最低点就是与
值的增大而增大,因此③也是正确的;函数图象的最低点就是与![]() 轴的两个交点,根据
轴的两个交点,根据![]() ,求出相应的
,求出相应的![]() 的值为
的值为![]() 或
或![]() ,因此④也是正确的;从图象上看,当
,因此④也是正确的;从图象上看,当![]() 或
或![]() ,函数值要大于当
,函数值要大于当![]() 时的
时的![]() ,因此⑤时不正确的;逐个判断之后,可得出答案.
,因此⑤时不正确的;逐个判断之后,可得出答案.
解:①∵![]() ,
,![]() 和
和![]() 坐标都满足函数
坐标都满足函数![]() ,∴①是正确的;
,∴①是正确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线![]() ,因此②也是正确的;
,因此②也是正确的;
③根据函数的图象和性质,发现当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大,因此③也是正确的;
值的增大而增大,因此③也是正确的;
④函数图象的最低点就是与![]() 轴的两个交点,根据
轴的两个交点,根据![]() ,求出相应的
,求出相应的![]() 的值为
的值为![]() 或
或![]() ,因此④也是正确的;
,因此④也是正确的;
⑤从图象上看,当![]() 或
或![]() ,函数值要大于当
,函数值要大于当![]() 时的
时的![]() ,因此⑤时不正确的;
,因此⑤时不正确的;
故答案是:4
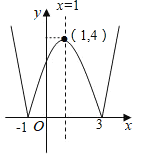


科目:初中数学 来源: 题型:
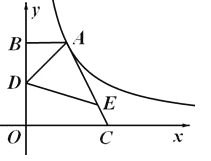
【题目】如图,点A在反比例函数y=![]() (x>0)的图象上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为6,则k的值为_____.
(x>0)的图象上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为6,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
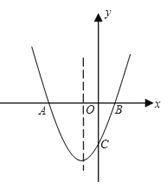
【题目】如图,抛物线y=mx2+2mx﹣3与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,且x2﹣x1=4.
(1)求抛物线的解析式;
(2)求抛物线的对称轴上存在一点P,使PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标.
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,D,E在△ABC的边BC上,若△ADE是等边三角形则称△ABC可内嵌,△ADE叫做△ABC的内嵌三角形.

(1)直角三角形______可内嵌.(填写“一定”、“一定不”或“不一定”)
(2)如图2,在△ABC中,∠BAC=120°,△ADE是△ABC的内嵌三角形,试说明AB2=BDBC是否成立?如果成立,请给出证明;如果不一定成立,请举例说明.
(3)在(2)的条件下,如果AB=1,AC=2,求△ABC的内嵌△ADE的边长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=12,AD平分∠BAC,交BC于点 E,交⊙O于点D,连接BD.

(1)求证:∠BAD=∠CBD;
(2)若∠AEB=125°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形ABCD的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
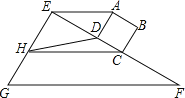
(1)当x=2时,AE的长为 ;
(2)试求出y关于x的函数关系式,并求出△EHD与△ADE的面积之差;
(3)当正方形ABCD移动时间x= 时,线段HD所在直线经过点B.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com