
【题目】在平面直角坐标系中,O为原点,点![]() ,点
,点![]() ,把
,把![]() 绕点B逆时针旋转,得
绕点B逆时针旋转,得![]() ,点A,O旋转后的对应点为
,点A,O旋转后的对应点为![]() ,
,![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(2)如图![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在![]() 的条件下,边OA上的一点P旋转后的对应点为
的条件下,边OA上的一点P旋转后的对应点为![]() ,当
,当![]() 取得最小值时,求点
取得最小值时,求点![]() 的坐标
的坐标![]() 直接写出结果即可
直接写出结果即可![]()

【答案】(1)![]()
(2)![]()
(3)![]()
【解析】
![]() 由旋转的性质可得
由旋转的性质可得![]() 为等腰直角三角形,再由勾股定理求出
为等腰直角三角形,再由勾股定理求出![]() 的长;
的长;
![]() 利用旋转的性质可得
利用旋转的性质可得![]() ,
,![]() ,则
,则![]() ,在
,在![]() 中利用含
中利用含![]() 的直角三角形三边的关系可计算出
的直角三角形三边的关系可计算出![]() 和
和![]() 的长,从而得到点
的长,从而得到点![]() 的坐标;
的坐标;
![]() 由旋转的性质得
由旋转的性质得![]() 利用两点之间线段最短可判断
利用两点之间线段最短可判断![]() 点过直线O
点过直线O![]() C时
C时![]() 最小,接着用待定系数法求出直线
最小,接着用待定系数法求出直线![]() 的解析式,从而求得
的解析式,从而求得![]() 点坐标,又因为
点坐标,又因为![]() ,作
,作![]() 于
于![]() ,然后根据含
,然后根据含![]() 的直角三角形三边的关系可计算出
的直角三角形三边的关系可计算出![]() ,
,![]() 的长,从而得到点
的长,从而得到点![]() 的坐标。
的坐标。
解:
![]() 如图①所示,
如图①所示,
![]() 点
点![]() ,点
,点![]()
![]() ,
,![]()
![]()
![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
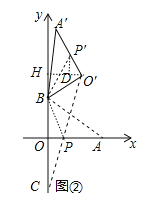
如图②,作![]() 轴于
轴于![]()
![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]()
![]() ,
,![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]() 点的坐标为
点的坐标为![]()
![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,点
,点![]() 的对应点为
的对应点为![]()
![]()
![]()
作![]() 点关于
点关于![]() 轴的对称点
轴的对称点![]() 连结
连结![]() 交
交![]() 轴于
轴于![]() 点,如图②
点,如图②
则![]() ,此时
,此时![]() 的值最小,
的值最小,
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
![]()
设直线O![]() C的解析式为
C的解析式为![]()
把![]() 代入得
代入得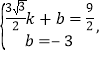 解得
解得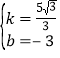
![]() 直线
直线![]() 的解析式为:
的解析式为:![]()
当![]() 时,
时,![]() ,解得:
,解得:![]()
![]()
![]() ,
,![]() ,
,
作P![]() 于
于![]() ,
,
![]()
![]()
![]()
![]()
![]() 坐标为:
坐标为:![]()
![]() 的坐标为
的坐标为![]()


科目:初中数学 来源: 题型:
【题目】某乡在推进村村通公路某项目建设中,计划修建公路15千米.已知甲队单独完成修建公路所需得时间是乙队得1.5倍,甲队每天比乙队少修0.5千米.
(1)求甲、乙两队单独完成修建公路各需多少天?
(2)已知甲队每天的工作费用是4000元,乙队每天的工作费用是5000元,若该工程由甲乙两队合作完成,且工程的总费用不超过52000元,求乙队至少要工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
(1)若![]() ,函数图象与
,函数图象与![]() 轴只有一个交点,求
轴只有一个交点,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,设
,设![]() 点的横坐标为
点的横坐标为![]() ,求证:
,求证:![]() ;
;
(3)若![]() ,
,![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 在
在![]() 时,
时,![]() 随
随![]() 的增大而增大?若存在,求
的增大而增大?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.将线段AB绕点B顺时针旋转90°,得线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.
(Ⅰ)作出旋转后的图形;
(Ⅱ) ![]() = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的 日销售量(件)与时间(天)的关系如下表:
时间(天) | 1 | 3 | 6 | 10 | 36 | … |
日销售量(件) | 94 | 90 | 84 | 76 | 24 | … |
未来40天内,前20天每天的价格y1(元/件)与t时间(天)的函数关系式为:y1=![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—
t+25(1≤t≤20且t为整数);后20天每天的价格y2(原/件)与t时间(天)的函数关系式为:y2=—![]() t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
t+40(21≤t≤40且t为整数).下面我们来研究 这种商品的有关问题.
(1)认真分析上表中的数量关系,利用学过的一次函数、二次函数 、反比例函数的知识确定一个满足这些数据之间的函数关系式;
(2)请预测未来40天中那一天的销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程,公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
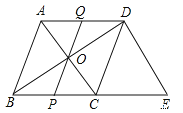
【题目】如图,在菱形ABCD中,对角线AC与BD相交于O点,AB=5,AC=6,过D点作DE//AC交BC的延长线于E点
(1)求△BDE的周长
(2)点P为线段BC上的点,连接PO并延长交AD于点Q,求证:BP=DQ
查看答案和解析>>
科目:初中数学 来源: 题型:
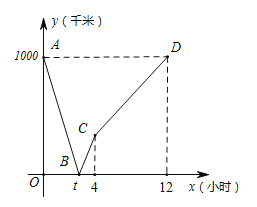
【题目】甲、乙两地高速铁路建设成功.试运行期间,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发.设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象分析出以下信息:①甲乙两地相距1000千米;②动车从甲地到乙地共需要4个小时;③![]() 表示的实际意义是动车的速度;④普通列车的速度是
表示的实际意义是动车的速度;④普通列车的速度是![]() 千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
A.①②④B.①③④⑤C.①②④⑤D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )

A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com