
【题目】如图,在四边形ABCD中,∠B=∠C=90°,∠DAB与∠ADC的平分线相交于BC边上的M点,则下列结论:①∠AMD=90°;②M为BC的中点;③AB+CD=AD;④ ![]() ;⑤M到AD的距离等于BC的一半;其中正确的有( )
;⑤M到AD的距离等于BC的一半;其中正确的有( )
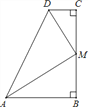
A. 2个 B. 3个 C. 4个 D. 5个
【答案】D
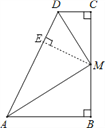
【解析】过M作ME⊥AD于E,
∵∠DAB与∠ADC的平分线相交于BC边上的M点,
∴∠MDE=∠MDC=![]() ∠CDA,∠MAD=∠MAB=
∠CDA,∠MAD=∠MAB=![]() ∠BAD,
∠BAD,
∵DC∥AB,∴∠CDA+∠BAD=180°,
∴∠MDA+∠MAD=![]() (∠CDA+∠BAD)=
(∠CDA+∠BAD)=![]() ×180°=90°,
×180°=90°,
∴∠AMD=180°-(∠MDA+∠MAD)=90°,∴①正确;
∵DM平分∠CDE,∠C=90°,ME⊥DA,
∴MC=ME,同理ME=MB,
∴MC=MB=ME=![]() BC,∴②正确;
BC,∴②正确;
∴M到AD的距离等于BC的一半,∴⑤正确;
∵在Rt△DEM和Rt△DCM中,MD=MD,ME=MC,
∴Rt△DEM≌Rt△DCM,∴DE=DC,S△DEM=S△DCM,
同理AE=AB,S△AEM=S△ABM,
∴AD=AE+ED=AB+CD;S△AMD=S△DEM+S△AEM=![]() S梯形ABCD,∴③④正确.
S梯形ABCD,∴③④正确.
综上①②③④⑤都正确,故选D.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
【题目】观察下列格式, ![]() -
- ![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
(1)化简以上各式,并计算出结果;
(2)以上格式的结果存在一定的规律,请按规律写出第5个式子及结果.
(3)用含n(n≥1的整数)的式子写出第n个式子及结果,并给出证明的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)在一次消防演习中,消防员架起一架25米长的云梯AB,如图斜靠在一面墙上,梯子底端B离墙角C的距离为7米。
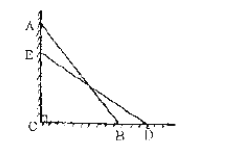
(1)求这个梯子的顶端距地面的高度AC是多少?
(2)如果消防员接到命令,按要求将梯子底部在水平方向滑 动后停在DE的位置上(云梯长度不变),测得BD长为8米,那么云梯的顶部在下滑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
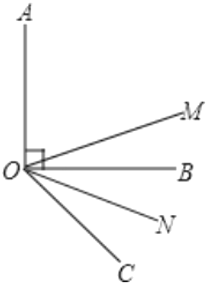
【题目】如图,已知![]() 与
与![]() 互为余角,且
互为余角,且![]() 平分
平分![]() 平分
平分![]() .
.
(1)求![]() 的度数;
的度数;
(2)如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;如果已知
_______度;如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;
_______度;
(3)从以上求![]() 的过程中,你得出的结论是__________.
的过程中,你得出的结论是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com