
ЎҫМвДҝЎҝОӘБЛИГС§ЙъНШХ№КУТ°Ўў·бё»ЦӘК¶Ј¬јУЙоУлЧФИ»әНОД»ҜөДЗЧҪьёР,ФцјУ¶ФјҜМеЙъ»о·ҪКҪәНЙз»б№«№ІөАөВөДМеСй,ОТЗшДіЦРС§ҫц¶ЁЧйЦҜІҝ·ЦКҰЙъИҘЛжЦЭСЧөЫ№КАпҝӘХ№СРС§ВГРР»о¶Ҝ.ФЪІОјУҙЛҙО»о¶ҜөДКҰЙъЦР,ИфГҝО»АПКҰҙш![]() ёцС§Йъ,»№КЈ
ёцС§Йъ,»№КЈ![]() ёцС§ЙъГ»ИЛҙш;ИфГҝО»АПКҰҙш
ёцС§ЙъГ»ИЛҙш;ИфГҝО»АПКҰҙш![]() ёцС§ЙъЈ¬ҫНУРТ»О»АПКҰЙЩҙш
ёцС§ЙъЈ¬ҫНУРТ»О»АПКҰЙЩҙш![]() ёцС§Йъ.ОӘБЛ°ІИ«,јИТӘұЈЦӨЛщУРКҰЙъ¶јУРіөЧш,УЦТӘұЈЦӨГҝБҫҝНіөЙПЦБЙЩТӘУР
ёцС§Йъ.ОӘБЛ°ІИ«,јИТӘұЈЦӨЛщУРКҰЙъ¶јУРіөЧш,УЦТӘұЈЦӨГҝБҫҝНіөЙПЦБЙЩТӘУР![]() ГыАПКҰ.ПЦУРјЧЎўТТБҪЦЦҙуҝНіөЈ¬ЛьГЗөДФШҝНБҝәНЧвҪрИзұнЛщКҫ.
ГыАПКҰ.ПЦУРјЧЎўТТБҪЦЦҙуҝНіөЈ¬ЛьГЗөДФШҝНБҝәНЧвҪрИзұнЛщКҫ.

ЈЁ1Ј©ІОјУҙЛҙОСРС§ВГРР»о¶ҜөДАПКҰУР ИЛЈ»С§ЙъУР ИЛЈ»ЧвУГҝНіөЧЬКэОӘ БҫЈ»
ЈЁ2Ј©ЙиЧвУГ![]() БҫТТЦЦҝНіөЈ¬Чвіө·СУГОӘ
БҫТТЦЦҝНіөЈ¬Чвіө·СУГОӘ![]() ФӘЈ¬ЗлРҙіц
ФӘЈ¬ЗлРҙіц![]() Ул
Ул![]() Ц®јдөДәҜКэ№ШПөКҪЈ»
Ц®јдөДәҜКэ№ШПөКҪЈ»
ЈЁ3Ј©ФЪЈЁ2Ј©өДМхјюПВЈ¬С§РЈјЖ»®ҙЛҙОСРС§ВГРР»о¶ҜөДЧвіөЧЬ·СУГІ»і¬№э![]() ФӘЈ¬ДгДЬөГіцДДјёЦЦІ»Н¬өДЧвіө·Ҫ°ёЈҝЖдЦРДДЦЦЧвіө·Ҫ°ёЧоКЎЗ®ЈҝЗлЛөГчАнУЙ.
ФӘЈ¬ДгДЬөГіцДДјёЦЦІ»Н¬өДЧвіө·Ҫ°ёЈҝЖдЦРДДЦЦЧвіө·Ҫ°ёЧоКЎЗ®ЈҝЗлЛөГчАнУЙ.
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»
Ј»![]() Ј»
Ј»![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]() Ј»ЈЁ3Ј©№ІУР
Ј»ЈЁ3Ј©№ІУР![]() ЦЦЧвіө·Ҫ°ёЈә·Ҫ°ёТ»ЈәЧвУГјЧЦЦҝНіө
ЦЦЧвіө·Ҫ°ёЈә·Ҫ°ёТ»ЈәЧвУГјЧЦЦҝНіө![]() БҫЈ¬ТТЦЦҝНіө
БҫЈ¬ТТЦЦҝНіө![]() БҫЈ»·Ҫ°ё¶юЈәЧвУГјЧЦЦҝНіө
БҫЈ»·Ҫ°ё¶юЈәЧвУГјЧЦЦҝНіө![]() БҫЈ¬ТТЦЦҝНіө
БҫЈ¬ТТЦЦҝНіө![]() БҫЈ»·Ҫ°ёИэЈәЧвУГјЧЦЦҝНіө
БҫЈ»·Ҫ°ёИэЈәЧвУГјЧЦЦҝНіө![]() БҫЈ¬ТТЦЦҝНіө
БҫЈ¬ТТЦЦҝНіө![]() БҫЈ»ЧоҪЪКЎ·СУГөДЧвіө·Ҫ°ёКЗЈәЧвУГјЧЦЦҝНіө
БҫЈ»ЧоҪЪКЎ·СУГөДЧвіө·Ҫ°ёКЗЈәЧвУГјЧЦЦҝНіө![]() БҫЈ¬ТТЦЦҝНіө
БҫЈ¬ТТЦЦҝНіө![]() БҫЈ»
БҫЈ»
ЎҫҪвОцЎҝ
ЈЁ1Ј©ЙиіцАПКҰУРxГыЈ¬С§ЙъУРyГыЈ¬өГіц¶юФӘТ»ҙО·ҪіМЧйЈ¬ҪвіцјҙҝЙЈ»
ЈЁ2Ј©ЙиУГ![]() БҫТТЈ¬ФтјЧЦЦҝНіөКэОӘЈә
БҫТТЈ¬ФтјЧЦЦҝНіөКэОӘЈә![]() БҫЈ¬ҙъИлјЖЛгјҙҝЙ
БҫЈ¬ҙъИлјЖЛгјҙҝЙ
ЈЁ3Ј©ЙиЧвУГxБҫТТЦЦҝНіөЈ¬ФтјЧЦЦҝНіөКэОӘЈәЈЁ8-xЈ©БҫЈ¬УЙМвТвөГіц400x+300ЈЁ8-xЈ©ЎЬ3100Ј¬өГіцxИЎЦө·¶О§Ј¬·ЦОцөГіцјҙҝЙЈ®
(1)ЙиАПКҰУРxГыЈ¬С§ЙъУРyГыЎЈ
ТАМвТвЈ¬БР·ҪіМЧй![]() Ј¬
Ј¬
ҪвөГ![]() Ј¬
Ј¬
ЎЯГҝБҫҝНіөЙПЦБЙЩТӘУР2ГыАПКҰЈ¬
ЎаЖыіөЧЬКэІ»ДЬі¬№э8БҫЈ»
УЦТӘұЈЦӨ300ГыКҰЙъУРіөЧш,ЖыіөЧЬКэІ»ДЬРЎУЪ![]() =
=![]() (ИЎХыОӘ8)БҫЈ¬
(ИЎХыОӘ8)БҫЈ¬
ЧЫәПЖрАҙҝЙЦӘЖыіөЧЬКэОӘ8БҫЈ»
ҙрЈәАПКҰУР16ГыЈ¬С§ЙъУР284ГыЈ»ЧвУГҝНіөЧЬКэОӘ8БҫЎЈ
ЈЁ2Ј©![]() ЧвУГ
ЧвУГ![]() БҫТТЈ¬
БҫТТЈ¬![]() јЧЦЦҝНіөКэОӘЈә
јЧЦЦҝНіөКэОӘЈә![]() БҫЈ¬
БҫЈ¬
![]() .
.
ЈЁ3Ј©![]() ЧвіөЧЬ·СУГІ»і¬№э
ЧвіөЧЬ·СУГІ»і¬№э![]() ФӘЈ¬ЧвУГТТЦЦҝНіөІ»ЙЩУЪ
ФӘЈ¬ЧвУГТТЦЦҝНіөІ»ЙЩУЪ![]() БҫЈ¬
БҫЈ¬
![]() Ј¬ҪвөГЈә
Ј¬ҪвөГЈә![]() Ј¬
Ј¬
ОӘК№![]() ГыКҰЙъ¶јУРЧщЈ¬
ГыКҰЙъ¶јУРЧщЈ¬![]() Ј¬
Ј¬
ҪвөГЈә![]() Ј¬
Ј¬
![]() ИЎХыКэОӘ
ИЎХыКэОӘ![]() .
.
![]() №ІУР
№ІУР![]() ЦЦЧвіө·Ҫ°ёЈә
ЦЦЧвіө·Ҫ°ёЈә
·Ҫ°ёТ»ЈәЧвУГјЧЦЦҝНіө![]() БҫЈ¬ТТЦЦҝНіө
БҫЈ¬ТТЦЦҝНіө![]() БҫЈ»
БҫЈ»
·Ҫ°ё¶юЈәЧвУГјЧЦЦҝНіө![]() БҫЈ¬ТТЦЦҝНіө
БҫЈ¬ТТЦЦҝНіө![]() БҫЈ»
БҫЈ»
·Ҫ°ёИэЈәЧвУГјЧЦЦҝНіө![]() БҫЈ¬ТТЦЦҝНіө
БҫЈ¬ТТЦЦҝНіө![]() БҫЈ»
БҫЈ»
УЙЈЁ2Ј©![]() Ј¬
Ј¬![]() Лж
Лж![]() өДјхРЎ¶шјхРЎЈ¬
өДјхРЎ¶шјхРЎЈ¬
![]() ЗТ
ЗТ![]() ОӘХыКэЈ¬
ОӘХыКэЈ¬![]() өұ
өұ![]() КұЈ¬
КұЈ¬![]() ФӘЈ¬
ФӘЈ¬
№КЧоҪЪКЎ·СУГөДЧвіө·Ҫ°ёКЗЈәЧвУГјЧЦЦҝНіө![]() БҫЈ¬ТТЦЦҝНіө
БҫЈ¬ТТЦЦҝНіө![]() БҫЈ»
БҫЈ»



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
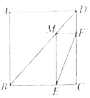
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ЎчACBәНЎчECD¶јКЗөИСьЦұҪЗИэҪЗРОЈ¬ЎПACBЈҪЎПECDЈҪ90ЎгЈ¬DОӘABұЯЙПТ»өгЈ®
(1)ЗуЦӨЈәЎчACEЎХЎчBCDЈ»
(2)ИфADЈҪ5Ј¬BDЈҪ12Ј¬ЗуDEөДіӨЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіөШЗшОӘБЛұЈ»ӨәНёДЙЖЙъМ¬»·ҫіЈ¬ҫц¶ЁҙУ2014ДкЖрҪшРРЎ°НЛёы»№БЦЎұЈ¬°СТЧФміЙЛ®НББчК§өДЖВёыөШұдОӘБЦөШЈ¬ІўіцМЁБЛТ»ПојӨАшҙлК©ЈәФЪЎ°НЛёы»№БЦЎұөД№эіМЦРЈ¬ГҝТ»ДкРВФцБЦөШГж»эҙпөҪ10Д¶өДЕ©»§Ј¬өұДк¶јҝЙөГөҪЙъ»оІ№Мщ1500ФӘЈ¬ЗТГҝі¬іцТ»Д¶Ј¬Хюё®»№ёшУиГҝД¶aФӘөДҪұАшЈ®БнНвЈ¬ҫӯЎ°НЛёы»№БЦЎұәуөДБЦөШҙУПВТ»ДкЖрЈ¬ЖҪҫщГҝД¶ГҝДкҝЙУР110ФӘөДЦЦКчКХИлЈ®ПВұнКЗДіЕ©»§ФЪН·БҪДкНЁ№эЎ°НЛёы»№БЦЎұГҝДк»сөГөДЧЬКХИлЈЁДкЧЬКХИлЈҪЙъ»оІ№Мщ·С+Хюё®ҪұАш·С+ЦЦКчКХИлЈ©ЗйҝцЈә
Дк·Э | РВФцБЦөШД¶Кэ | ДкЧЬКХИл |
2014 | 20Д¶ | 2400 |
2015 | 26Д¶ | 4300ФӘ |
ЈЁ1Ј©КФёщҫЭТФЙПМṩөДЧКБПЗуaөДЦөЈ»
ЈЁ2Ј©Из№ыёГЕ©»§јЖ»®ФЪ2016ДкЧЬКХИлҙпөҪ10000ФӘЈ¬ФтёГЕ©»§ФЪ2016ДкУҰРВФцБЦөШФј¶аЙЩД¶ЈҝЈЁҪб№ыұЈБфХыКэЈ©
ЈЁ3Ј©ҙУ2015ДкЖрЈ¬Из№ыёГЕ©»§ГҝДкРВФцБЦөШөДД¶КэҫщДЬұИЗ°Т»Дк°ҙПаН¬өДФціӨВКФціӨЈ¬ДЗГҙёГЕ©»§ФЪ2017ДкРВФцБЦөШ¶аЙЩД¶ЈЁҪб№ыұЈБфБҪО»РЎКэЈ©Јҝ2017ДкёГЕ©»§НЁ№эЎ°НЛёы»№БЦЎұ»сөГөДДкЧЬКХИлҪ«ҙпөҪ¶аЙЩФӘЈЁҪб№ыұЈБфТ»О»РЎКэЈ©Јҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЎчABCУлЎчAЎдBЎдCЎдФЪЖҪГжЦұҪЗЧшұкПөЦРөДО»ЦГИзНјЈ®

ЈЁ1Ј©·ЦұрРҙіцПВБРёчөгөДЧшұкЈә AЎдЎЎ ЎЎЈ»BЎдЎЎ ЎЎЈ»CЎдЎЎ ЎЎЈ»
ЈЁ2Ј©ИфөгPЈЁaЈ¬bЈ©КЗЎчABCДЪІҝТ»өгЈ¬ФтЖҪТЖәуЎчAЎдBЎдCЎдДЪөД¶ФУҰөгPЎдөДЧшұкОӘЎЎ ЎЎЈ»
ЈЁ3Ј©ЗуЎчABCөДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪұЯіӨОӘ![]() өДХэ·ҪРО
өДХэ·ҪРО![]() ЦРЈ¬өг
ЦРЈ¬өг![]() ОӘ¶ФҪЗПЯ
ОӘ¶ФҪЗПЯ![]() ЙПТ»¶ҜөгЈ¬
ЙПТ»¶ҜөгЈ¬![]() УЪ
УЪ![]() УЪ
УЪ![]() Ј¬Фт
Ј¬Фт![]() өДЧоРЎЦөОӘЈЁ Ј©
өДЧоРЎЦөОӘЈЁ Ј©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіЗаҙәөіЦ§ІҝФЪҫ«Чј·цЖ¶»о¶ҜЦРЈ¬ёшҪб¶Ф°п·цөДЖ¶А§јТНҘФщЛНјЧЎўТТБҪЦЦКчГзИГЖдФФЦЦЈ®ТСЦӘТТЦЦКчГзөДјЫёсұИјЧЦЦКчГз№у10ФӘЈ¬УГ480ФӘ№әВтТТЦЦКчГзөДҝГКэЗЎәГУлУГ360ФӘ№әВтјЧЦЦКчГзөДҝГКэПаН¬Ј®
ЈЁ1Ј©ЗујЧЎўТТБҪЦЦКчГзГҝҝГөДјЫёсёчКЗ¶аЙЩФӘЈҝ
ЈЁ2Ј©ФЪКөјК°п·цЦРЈ¬ЛыГЗҫц¶ЁФЩҙО№әВтјЧЎўТТБҪЦЦКчГз№І50ҝГЈ¬ҙЛКұЈ¬јЧЦЦКчГзөДКЫјЫұИөЪТ»ҙО№әВтКұҪөөНБЛ10%Ј¬ТТЦЦКчГзөДКЫјЫІ»ұдЈ¬Из№ыФЩҙО№әВтБҪЦЦКчГзөДЧЬ·СУГІ»і¬№э1500ФӘЈ¬ДЗГҙЛыГЗЧо¶аҝЙ№әВт¶аЙЩҝГТТЦЦКчГзЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪКэЦбЙПөгAұнКҫКэaЈ¬өгBұнКҫКэbЈ¬өгCұнКҫКэcЈ®bКЗЧоРЎөДХэХыКэЈ¬ЗТaЎўbВъЧг|a+2|+ЈЁc©Ғ7Ј©2=0
ЈЁ1Ј©МоҝХЈәa=ЎЎ ЎЎЈ¬b=ЎЎ ЎЎЈ®
ЈЁ2Ј©өгAЎўBЎўCҝӘКјФЪКэЦбЙПФЛ¶ҜЈ¬ИфөгAТФГҝГл1ёцөҘО»іӨ¶ИөДЛЩ¶ИПтЧуФЛ¶ҜЈ¬Н¬КұЈ¬өгBәНөгC·ЦұрТФГҝГл2ёцөҘО»іӨ¶ИәН4ёцөҘО»іӨ¶ИөДЛЩ¶ИПтУТФЛ¶ҜЈ¬јЩЙиtГлЦУ№эәуЈ¬ИфөгAУлөгBЦ®јдөДҫаАлұнКҫОӘABЈ¬өгAУлөгCЦ®јдөДҫаАлұнКҫОӘACЈ¬өгBУлCЦ®јдөДҫаАлұнКҫОӘBCЈ®ФтBC=ЎЎ ЎЎЈ®ЈЁУГә¬tөДҙъКэКҪұнКҫЈ©
ЈЁ3Ј©ЗлОКЈә|2AB©Ғ3BC|өДЦөКЗ·сЛжЧЕКұјдtөДұд»Ҝ¶шёДұдЈҝИфёДұдЈ¬ЗлЛөГчАнУЙЈ»ИфІ»ұдЈ¬ЗлЗуЖдЦөЈ®
![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
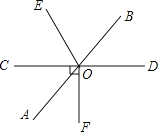
ЎҫМвДҝЎҝИзНјЈ¬ЦұПЯABЈ¬CDПаҪ»УЪөгOЈ¬OEЖҪ·ЦЎПBOCЈ¬ЎПCOFЈҪ90ЎгЈ®
ЈЁ1Ј©ИфЎПBOEЈҪ65ЎгЈ¬ЗуЎПAOFөД¶ИКэЈ»
ЈЁ2Ј©ИфЎПBODЈәЎПBOEЈҪ1Јә2Ј¬ЗуЎПAOFөД¶ИКэ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
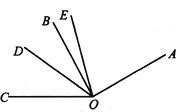
ЎҫМвДҝЎҝИзНјЈ¬ODКЗЎПBOCөДЖҪ·ЦПЯЈ¬OEКЗЎПAOCөДЖҪ·ЦПЯЈ¬ЎПAOB©UЎПBOC=3©U2Ј¬ИфЎПBOE=13ЎгЈ¬ЗуЎПDOEөД¶ИКэ.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com