
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
【答案】(1)A′(﹣3,1),B′(﹣2,﹣2)、C′(﹣1,﹣1);(2)(a﹣4,b﹣2);(3)2.
【解析】
(1)根据平面直角坐标系的特点直接写出坐标;
(2)首先根据A与A′的坐标观察变化规律,P的坐标变换与A点的变换一样,可写出点P′的坐标;
(3)先求出△ABC所在的矩形的面积,然后减去△ABC四周的三角形的面积即可.
解:(1)由图可知: A′(﹣3,1),B′(﹣2,﹣2)、C′(﹣1,﹣1);
(2)A(1,3)变换到点A′的坐标是(﹣3,1),
横坐标减4,纵坐标减2,
∴点P的对应点P′的坐标是(a﹣4,b﹣2);
(3)△ABC的面积为:3×2﹣![]() ×2×2﹣
×2×2﹣![]() ×3×1﹣
×3×1﹣![]() ×1×1=2.
×1×1=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F.求证:(1)△ACE≌△BCD;(2)![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对两实数![]() ,
,![]() 定义一种新运算,规定
定义一种新运算,规定![]() .
.
例如:![]() .
.
(1)填空:![]() ________;
________;![]() ________.
________.
(2)若![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,
,![]() 为整数,且
为整数,且![]() ,求满足条件的所有
,求满足条件的所有![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线相交于点O.以AB、AO为邻边画平行四边形AOC1B,对角线相交于点O ;以AB、AO 为邻边画平行四边形AO1C2B,对角线相交于点O2 :……以此类推,则平行四边形AO4C5B的面积为( )

A.![]() cm2B.
cm2B.![]() cm2C.
cm2C.![]() cm2D.
cm2D. ![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
(1)求证:AB与⊙O相切;
(2)若AB=4,求线段GF的长.
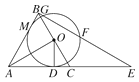
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明晚饭后外出散步,遇见同学,交谈一会,返回途中在读报厅看了一会报.下图是根据此情景画出的图象,请你回答下列问题:
(1)小明在距家多远遇见同学的,交谈了多少时间?
(2)读报厅离家多远?
(3)小明在哪一段路程中走得最快,速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:基本不等式![]() ≤
≤![]() (a>0,b>0),当且仅当a=b时,等号成立.其中我们把
(a>0,b>0),当且仅当a=b时,等号成立.其中我们把![]() 叫做正数a、b的算术平均数,
叫做正数a、b的算术平均数,![]() 叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵x>0,![]() >0∴
>0∴![]() ≥
≥![]() 即是x+
即是x+![]() ≥2
≥2![]()
∴x+![]() ≥2
≥2
当且仅当x=![]() 即x=1时,x+
即x=1时,x+![]() 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若x>0,函数y=2x+![]() ,当x为何值时,函数有最小值,并求出其最小值.
,当x为何值时,函数有最小值,并求出其最小值.
(2)当x>0时,式子x2+1+![]() ≥2成立吗?请说明理由.
≥2成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m,离开水面1.5 m处是涵洞宽ED.
(1)求抛物线的解析式;
(2)求ED的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com