
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点,与y轴交于点C,点O为坐标原点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,点D为直线AE上方抛物线上的一点
(1)求抛物线所对应的函数解析式;
(2)求△ADE面积的最大值和此时点D的坐标;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.

【答案】(1)y=﹣x2+2x+3;(2)△ADE面积的最大值是![]() ,D(
,D(![]() ,
,![]() );(3)点G不在该抛物线上,见解析
);(3)点G不在该抛物线上,见解析
【解析】
![]() 确定点C、点E的坐标,并代入二次函数表达式,即可求解;
确定点C、点E的坐标,并代入二次函数表达式,即可求解;
![]() 设
设![]() ,利用
,利用![]() ,将△ADE面积表示为
,将△ADE面积表示为![]() 的二次函数,用配方法即可求出面积的最值;
的二次函数,用配方法即可求出面积的最值;
![]() 绕点C逆时针旋转
绕点C逆时针旋转![]() ,OC落在CE所在的直线上,点A的对应点G的坐标为
,OC落在CE所在的直线上,点A的对应点G的坐标为![]() ,即可用验根法判断.
,即可用验根法判断.
解:![]() 四边形OCEF为矩形,
四边形OCEF为矩形,![]() ,
,![]() ,
,
![]() 点C的坐标为
点C的坐标为![]() ,点E的坐标为
,点E的坐标为![]() ,
,
把![]() ,
,![]() ;
;![]() ,
,![]() ,分别代入二次函数表达式得:
,分别代入二次函数表达式得:![]() ,解得:
,解得:![]() ,
,![]() 抛物线对应函数的表达式为:
抛物线对应函数的表达式为:![]() ;
;
![]() 连接DF、DE、DA,
连接DF、DE、DA,
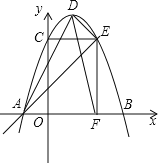
![]() 点D在直线AE上方的抛物线上,∴
点D在直线AE上方的抛物线上,∴![]() ,
,
令![]() ,得:
,得:![]() ,解得:
,解得:![]() 或3,
或3,
![]() 、
、![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 面积的最大值是
面积的最大值是![]() ,
,
此时![]() ,
,![]() ,
,
此时点D的坐标为![]() ;
;
![]() 绕点C逆时针旋转
绕点C逆时针旋转![]() ,OC落在CE所在的直线上,
,OC落在CE所在的直线上,
由![]() 知
知![]() ,
,![]() 点A的对应点G的坐标为
点A的对应点G的坐标为![]() ,
,
当![]() 时,
时,![]() ,
,![]() 点G不在该抛物线上.
点G不在该抛物线上.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
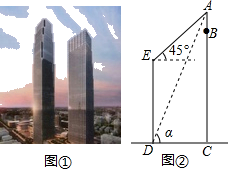
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,边
,边![]() 的长为
的长为![]() 边
边![]() 的长为
的长为![]() ,在此三角形内有一个矩形
,在此三角形内有一个矩形![]() ;点
;点![]() 分别在
分别在![]() 上,设
上,设![]() 的长为
的长为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() (单位:
(单位: ![]() )
)
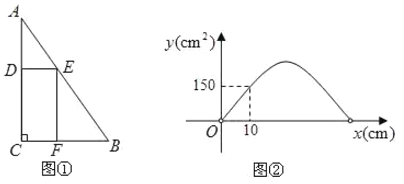
(1)当![]() 等于30时,求
等于30时,求![]() 与
与![]() 的函数关系式:(不要求写出自变量
的函数关系式:(不要求写出自变量![]() 的取值范围)
的取值范围)
(2)在(1)的条件下,矩形![]() 的面积能否为
的面积能否为![]() ?请说明理由?
?请说明理由?
(3)若![]() 与
与![]() 的函数图象如图2所示,求此时
的函数图象如图2所示,求此时![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市今年 1 月份的销售额为 500 万元,超市预计每个月的销售额会逐月增加.预测 3 月 份的销售额比 2 月份增加 120 万元;
(1)求 2、3 月份平均每月销售额的增长率;
(2)按照这样的增长速度,超市想在第一季度完成 1800 万元的销售目标是否能实现?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
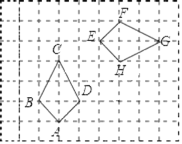
【题目】如图,四边形EFGH是由四边形ABCD经过旋转得到的,如果用有序数对(3,1)表示方格纸上A点的位置,用(2,2)表示点B的位置,那么由四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示为_____(数为整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10,动点E、F分别在边AB、AD上,且AF=![]() AE.将△AEF绕点E顺时针旋转90°得到△A'EF',设AE=x,△A'EF'与矩形ABCD重叠部分面积为S,S的最大值为9.
AE.将△AEF绕点E顺时针旋转90°得到△A'EF',设AE=x,△A'EF'与矩形ABCD重叠部分面积为S,S的最大值为9.
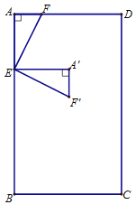
(1)求AD的长;
(2)求S关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
(1)求证:直线AB是⊙O的切线;
(2)OA,OB分别交⊙O于点D,E,AO的延长线交⊙O于点F,若AB=4AD,求sin∠CFE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.

(1)请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;
(2)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;
(3)开动脑筋想一想,相信你能求出经过点D的“蛋圆”切线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
如图1.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,可以得到:
![]()
证明:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,![]()
∴![]()
∴![]()
同理:![]()
![]()
∴![]()
(1)通过上述材料证明:
![]()
(2)运用(1)中的结论解决问题:
如图2,在![]() 中,
中,![]() ,求AC的长度.
,求AC的长度.
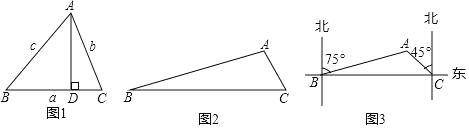
(3)如图3,为了开发公路旁的城市荒地,测量人员选择A、B、C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达C点,测得A在北偏西45°方向上,根据以上信息,求A、B、C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9,![]() ≈1.4,结果取整数)
≈1.4,结果取整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com