
【题目】如图,直线![]() 与⊙O相切于点D,过圆心O作EF∥
与⊙O相切于点D,过圆心O作EF∥![]() 交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线
交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线![]() 于B、C两点;
于B、C两点;
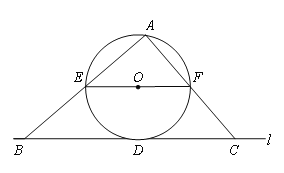
(1)求证:∠ABC+∠ACB=90°;
(2)若⊙O的半径![]() ,BD=12,求tan∠ACB的值.
,BD=12,求tan∠ACB的值.
【答案】(1)详见解析(2)tan∠ACB![]()
【解析】
(1)由直径所对圆周角是直角的性质和三角形内角和定理可得结论。
(2)求出tan∠BEH=![]() ,由∠ACB=∠BEH可得结论。
,由∠ACB=∠BEH可得结论。
解(1)证明:如图,∵EF是⊙O的直径,∴∠EAF=90°。∴∠ABC+∠ACB=90°。
(2)连接OD,则OD⊥BD,过点E作EH⊥BC,垂足为点H,
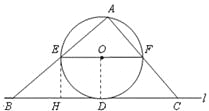
∴ EH∥OD。
∵EF∥BC,EH∥OD, OE=OD,
∴四边形EODH是正方形 。∴EH=HD=OD=5。
∵BD=12,∴BH=7。
在Rt△BEH中,tan∠BEH=![]() 。
。
又∵∠ABC+∠BEH=90°,∠ABC+∠ACB=90°,
∴∠ACB=∠BEH。∴tan∠ACB![]() 。
。


科目:初中数学 来源: 题型:
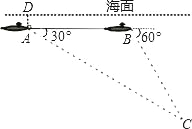
【题目】如图,在A处有一艘潜艇,并测得在俯视角为30°的方向有黑匣子,此时潜艇距海平面500米,继续在同一深度沿直线航行3000米后再次在B点出测得俯视角为60°正前方的海底黑匣子,求海底黑匣子所处位置C点出距离海面的深度.(保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
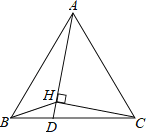
【题目】如图,△ABC是等边三角形,AB=![]() ,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
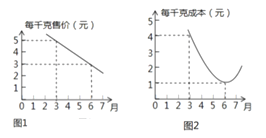
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( ).
A.一个三角形中至少有两个锐角
B.一个三角形中,一定有一个外角大于其中的一个内角
C.钝角三角形中至少有一个钝角
D.锐角三角形,任何两个内角的和均大于90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
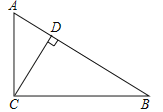
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,
(1)尺规作图:作△ABC的角平分线AE,交CD于点F(不写作法,保留作图痕迹);
(2)求证:△CEF为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com