
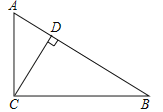
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,
(1)尺规作图:作△ABC的角平分线AE,交CD于点F(不写作法,保留作图痕迹);
(2)求证:△CEF为等腰三角形.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与⊙O相切于点D,过圆心O作EF∥
与⊙O相切于点D,过圆心O作EF∥![]() 交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线
交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线![]() 于B、C两点;
于B、C两点;
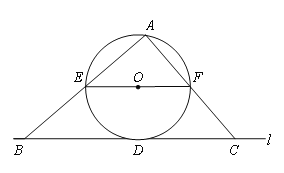
(1)求证:∠ABC+∠ACB=90°;
(2)若⊙O的半径![]() ,BD=12,求tan∠ACB的值.
,BD=12,求tan∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( )
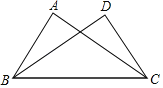
A.∠ABC=∠DCBB.∠ABD=∠DCA
C.AC=DBD.AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一个交点分别为M、N,如果点A与点B,点M与点N都关于原点O成中心对称,则抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是_______________________和_________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次“寻宝”人找到了如图所示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都是![]() ,则“宝藏”点的坐标是( )
,则“宝藏”点的坐标是( )
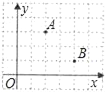
A. (1,0) B. (5,4) C. (1,0)或(5,4) D. (0,1)或(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓄水池的排水管每小时排水8立方米,6小时可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果每小时排水量用Q表示,求排水时间t与Q的函数关系式.
(3)如果5小时内把满池水排完,那么每小时排水量至少是多少?
(4)已知排水管最大排水量是每小时12立方米,那么最少要多少小时才能将满池水全部排空?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com