
【题目】如图,△ABC中,A(﹣2,3),B(﹣3,1),C(﹣1,2). 
(1)①将△ABC向右平移4个单位长度,画出平移后的△A1B1C1;
②画出△ABC关于x轴对称的△A2B2C2;
③将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;
(2)在△A1B1C1 , △A2B2C2 , △A3B3C3中,△与△成轴对称,对称轴是;△与△成中心对称,对称中心的坐标是 .
【答案】
(1)解:①△A1B1C1如图所示
②△A2B2C2如图所示
③△A3B3C3如图所示
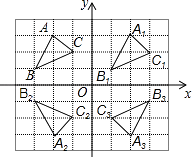
(2)A2B2C2 ;A3B3C3 ;y轴;A1B1C1 ;A3B3C3 ;(2,0)
【解析】解:(1)如图所示;(2)由图可知:△A2B2C2与△A3B3C3呈轴对称,且对称轴为y轴;
△A1B1C1与△A3B3C3呈中心对称,且对称中心为(2,0).
所以答案是:A2B2C2 , A3B3C3 , y轴;A1B1C1 , A3B3C3 , (2,0).
【考点精析】根据题目的已知条件,利用作轴对称图形的相关知识可以得到问题的答案,需要掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线.


科目:初中数学 来源: 题型:
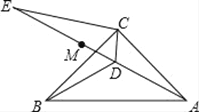
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 出发以每秒
出发以每秒![]() 个单位的速度在线段
个单位的速度在线段![]() 上从点
上从点![]() 向点
向点![]() 运动,点
运动,点![]() 同时从
同时从![]() 出发以每秒
出发以每秒![]() 个单位的速度在线段
个单位的速度在线段![]() 上向点
上向点![]() 运动,连接
运动,连接![]() 、
、![]() ,设
,设![]() 、
、![]() 两点运动时间为
两点运动时间为![]() 秒
秒![]() .
.
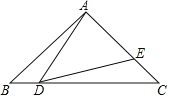
(1)运动 秒时,![]() ;
;
(2)运动多少秒时,![]() ≌
≌![]() 能成立;
能成立;
(3)若![]() ≌
≌![]() ,
,![]() ,求
,求![]() 的大小.(用含
的大小.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
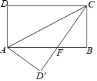
【题目】如图,长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在D′处.
(1)求证:△AFD′≌△CFB;
(2)求线段BF的长度;
(3)试求出重叠部分△AFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a+2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )
A.①②
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元函数y=﹣2x+m和反比例函数y= ![]() 的图象都经过点A(﹣2,1).
的图象都经过点A(﹣2,1).
(1)求一次函数和反比例函数的解析式;
(2)求一次函数与反比例函数的另一个交点B的坐标;
(3)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com