
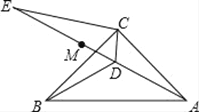
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
【答案】(1)详见解析;(2)①详见解析;②:ME=BD,证明详见解析;③∠CNE的度数为7.5°、15°、82.5°、150°.
【解析】
(1)根据中垂线的判定定理“与一条线段两个端点距离相等的点,在这条线段的垂直平分线上”可得出结论.
(2)①由∠CAD=15°,BD=AD与直角等腰三角形的性质可知,∠DBA=∠DAB=30°,则可得∠BDE=30°+30°=60°,又根据SSS可证△ADC≌△BDC,则∠ACD=∠BCD=45°,可知∠CDE=∠ACD+∠CAD=45°+15°=60°,故DE平分∠BDC.
②连接MC,由DC=DM,∠CDE=60°,可知△MCD为等边三角形,∠ECM=∠CMD-∠CAD=45°则根据SAS可证△BDC≌△EMC,得出结论ME=BD.
③根据题意可知,分类:当EN=EC时;当EN=CN时;当CE=CN时三种情况求出∠CNE的度数.
(1)证明:∵CB=CA,DB=DA,
∴CD垂直平分线段AB,
∴CD⊥AB,
故答案为:CD⊥AB.
(2)①证明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵在△ADC和△BDC中,
 ,
,
∴△ADC≌△BDC(SSS),
∴∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵∠ACB=90°,∠ACD=∠BCD,
∴∠ACD=∠BCD=45°,
∴∠CDE=∠ACD+∠CAD=45°+15°=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
故答案为:DE平分∠BDC.
②结论:ME=BD,
理由:连接MC,

∵DC=DM,∠CDE=60°,
∴△MCD为等边三角形,
∴CM=CD,∠CMD=60°,
又∵EC=CA,∠CAD=15°,
∴∠ECM=∠CMD-∠CAD=45°,
在△BDC和△EMC中,
 ,
,
∴△BDC≌△EMC(SAS),
∴ME=BD,
故答案为:ME=BD.
③当EN=EC时,∠ENC=7.5°或82.5°;
当EN=CN时,∠ENC=150°;
当CE=CN时,∠CNE=15°,
故答案为:∠CNE的度数为7.5°、15°、82.5°、150°.


科目:初中数学 来源: 题型:
【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN. 
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE:CD=5:24
(1)求CD的长;
(2)现汛期来临,水面要以每小时4m的速度上升,则经过多长时间桥洞会刚刚被灌满?
查看答案和解析>>
科目:初中数学 来源: 题型:
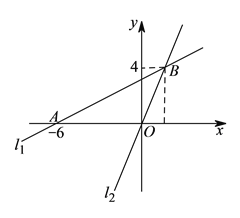
【题目】如图,在平面直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 与直线
与直线![]() ;
;![]() 相交于点
相交于点![]() .
.
(![]() )求直线
)求直线![]() 的表达式.
的表达式.
(![]() )过动点
)过动点![]() 且垂于
且垂于![]() 轴的直线与
轴的直线与![]() 、
、![]() 的交点分别为
的交点分别为![]() ,
,![]() ,当点
,当点![]() 位于点
位于点![]() 上方时,写出
上方时,写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN. 
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠C=90°,BC=6cm,AC=8 cm,AB=10 cm. 现有一动点P,从A点出发,沿着三角形的边AC-CB-BA运动,回到A点停止,速度为1 cm/s,设运动时间为t s.
(1)当t=_______时,△ABC的周长被线段AP平分为相等的两部分.
(2)当t=_______时,△APC的面积等于△ABC面积的一半.
(3)还有一个△DEF,∠E=90°,如图②所示,DE=4cm,DF=5cm,∠D=∠A. 在△ABC的边上,若另外有一个动点Q,与P 同时从A点出发,沿着边AB-BC-CA运动,回到点A停止. 在两点运动过程中某一时刻,恰好△APQ与△DEF全等,则点Q的运动速度 cm/s.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地. 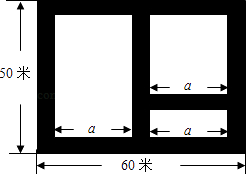
(1)设通道的宽度为x米,则a=(用含x的代数式表示);
(2)若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A(﹣2,3),B(﹣3,1),C(﹣1,2). 
(1)①将△ABC向右平移4个单位长度,画出平移后的△A1B1C1;
②画出△ABC关于x轴对称的△A2B2C2;
③将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;
(2)在△A1B1C1 , △A2B2C2 , △A3B3C3中,△与△成轴对称,对称轴是;△与△成中心对称,对称中心的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com