
【题目】如图,长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在D′处.
(1)求证:△AFD′≌△CFB;
(2)求线段BF的长度;
(3)试求出重叠部分△AFC的面积.
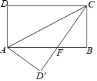
【答案】(1)见解析;(2)BF=3;(3)10.
【解析】
(1)由翻折的性质可得AD’=CB,再由对顶角可得∠AFD’=∠CFB,再∠D’=∠B=90°,则可证两三角形全等;
(2)设BF为x,则由三角形全等可得CF=AF=8-x,题干已知BC=4,故利用勾股定理BC2+FB2=CF2可求解;
(3)求解出AF长度,以AF为底,BC长度为高,利用三角形面积公式即可求解.
解:(1)由折叠可得,∠D'=∠D=∠B=90°,AD'=AD=BC,
在△AD'F和△CBF中,
∵∠AFD’=∠CFB,∠D’=∠B=90°,AD’=CB,
∴△AFD≌△CFB(AAS);
(2)由折叠可得,∠ACF=∠ACD,
∵CD∥AB,
∴∠CAF=∠ACD,
∴∠ACF=∠CAF,
∴AF=CF,
设BF=x,则AF=CF=8﹣x,
∵∠B=90°,
∴在Rt△BCF中,BF2+CB2=CF2,
即42+x2=(8﹣x)2,
解得x=3,
∴BF=3;
(3)∵AF=8﹣3=5,BC=4,CB⊥AF,
∴S△ACF=![]() AF×BC=
AF×BC=![]() ×5×4=10.
×5×4=10.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN. 
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数. 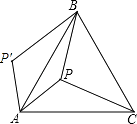
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系种中,点![]()
![]() 点
点![]() 关于
关于![]() 轴对称的点的坐标是:________;
轴对称的点的坐标是:________;
![]() 点
点![]() 关于
关于![]() 轴对称的点的坐标是:________;
轴对称的点的坐标是:________;
![]() 点
点![]() 关于原点对称的点的坐标是:________;
关于原点对称的点的坐标是:________;
![]() 将点
将点![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后,得到的点的坐标是:________;
后,得到的点的坐标是:________;
![]() 将点
将点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 后,得到的点的坐标是:________;
后,得到的点的坐标是:________;
![]() 将点
将点![]() 绕另一点
绕另一点![]() 旋转
旋转![]() 得到点
得到点![]() ,则
,则![]() 点的坐标为________.
点的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A(﹣2,3),B(﹣3,1),C(﹣1,2). 
(1)①将△ABC向右平移4个单位长度,画出平移后的△A1B1C1;
②画出△ABC关于x轴对称的△A2B2C2;
③将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;
(2)在△A1B1C1 , △A2B2C2 , △A3B3C3中,△与△成轴对称,对称轴是;△与△成中心对称,对称中心的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知非直角三角形ABC中,∠A=45°,高BD与CE所在直线交于点H,则∠BHC的度数是( )
A. 45° B. 45° 或125° C. 45°或135° D. 135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,AD与BE相交于点F,且AE=CD.
(1)求证:AD=BE;
(2)求∠BFD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB边的垂直平分线![]() 交BC于D,AC边的垂直平分线
交BC于D,AC边的垂直平分线![]() 交BC于E,
交BC于E, ![]() 与
与![]() 相交于点O,△ADE的周长为6cm.
相交于点O,△ADE的周长为6cm.
(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com