
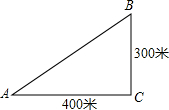
 如图,某海滨浴场岸边A处的救生员发现海中B处有人求救,若救生员在岸边行进的速度是8m/s,在海中行进的速度是2m/s,为了节约时间,救生员是直接游向B,还是沿岸边从A处跑到离B最近的点C,然后从点C游向B呢?你能通过计算帮救生员确定营救方案吗?
如图,某海滨浴场岸边A处的救生员发现海中B处有人求救,若救生员在岸边行进的速度是8m/s,在海中行进的速度是2m/s,为了节约时间,救生员是直接游向B,还是沿岸边从A处跑到离B最近的点C,然后从点C游向B呢?你能通过计算帮救生员确定营救方案吗?| 4002+3002 |
| 500 |
| 2 |
| 400 |
| 8 |
| 300 |
| 2 |


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
 如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )
如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
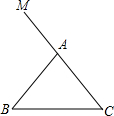 如图,在△ABC中,AB=AC,点M在CA的延长线上.
如图,在△ABC中,AB=AC,点M在CA的延长线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com