
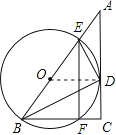
【题目】在Rt△ABC中,BC=9, CA=12,∠ABC的平分线BD交AC与点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连结EF,求![]() 的值.
的值.

【答案】(1)见详解;
(2)![]() .
.
【解析】
(1)因为点D在⊙O上,所以只要连结圆心和圆上这点,证明OD和AC垂直即可.
利用角平分线、等腰三角形、直角三角形两锐角互余,完成证明.
(2)利用勾股定理求得AB的长.;利用△ADO∽△ACB对应线段成比例求得BE的长;利用△BEF∽△BAC得![]() =
=![]() ,从而问题得解.
,从而问题得解.
(1)证明:由已知DE⊥DB,⊙O是Rt△BDE的外接圆,
∴BE是⊙O的直径,点O是BE的中点,连结OD,
∵![]() ,∴
,∴![]() .
.
又∵BD为∠ABC的平分线,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,即∴
,即∴![]()
又∵OD是⊙O的半径,
∴AC是⊙O的切线.
(2) 解:设⊙O的半径为r, 在Rt△ABC中,![]() ,
,
∴![]()
∵![]() ,
,![]() ,∴△ADO∽△ACB.
,∴△ADO∽△ACB.
∴![]() .∴
.∴![]() .
.
∴![]() .∴
.∴![]()
又∵BE是⊙O的直径.∴![]() .∴△BEF∽△BAC
.∴△BEF∽△BAC
∴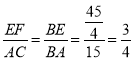 .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】为落实素质教育要求,促进学生全面发展,我市某中学2016年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2018年投资18.59万元.
(1)求该学校为新增电脑投资的年平均增长率;
(2)从2016年到2018年,该中学三年为新增电脑共投资多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司以22元/千克的成本价购进1000kg苹果,公司想知道苹果的损坏率,随机抽取若干进行统计,部分结果如下表:
草果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.60 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.106 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
根据此表估计这批苹果损坏的概率(精确到0.1),从而计算该公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应至少定为_____元/千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
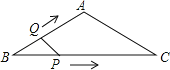
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A.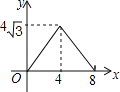 B.
B.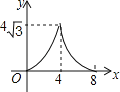
C.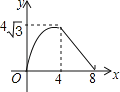 D.
D.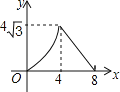
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
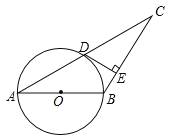
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若AC=16,tanA=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
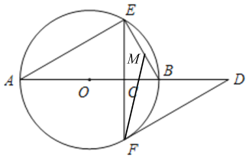
【题目】如图,AB是⊙O的直径,弦EF⊥AB,垂足为C,∠A=30°,连结BE,M为BE的中点,连结MF,过点F作直线FD∥AE,交AB的延长线于点D.
(1)求证:FD是⊙O的切线;
(2)若MF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
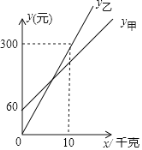
【题目】甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推岀优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠:乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓按售价付款,优惠期间,设游客的草莓采摘量为x(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙元,y甲、y乙与x之间的函数关系如图所示.
(1)求y甲、y乙与x的函数表达式;
(2)在春节期间,李华一家三口准备去草莓园采摘草莓,采摘的草莓合在一起支付费用,则李华一家应选择哪家草莓园更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com