
【题目】如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
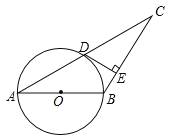
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若AC=16,tanA=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)DE为⊙O的切线;理由见解析;(2)5.
【解析】
(1)连接DO,BD,由∠BDE=∠A,∠A=∠ADO,得到∠ADO=∠EDB,再由圆周角定理得∠ADB=90°,得到∠ADO+∠ODB=90°,于是有∠ODB+∠EDB=90°,然后由切线的判定定理可判断DE为⊙O的切线;
(2)由等角的余角相等得到∠ABD=∠EBD,由于BD⊥AC,得到△ABC为等腰三角形,所以AD=CD=![]() AC=8,在Rt△ABD中利用正切定义可计算出BD的长,再由勾股定理计算出AB,从而得到⊙O的半径.
AC=8,在Rt△ABD中利用正切定义可计算出BD的长,再由勾股定理计算出AB,从而得到⊙O的半径.
解:(1)DE与⊙O相切.理由如下:
连接DO,BD,如图,
∵∠BDE=∠A,∠A=∠ADO,
∴∠ADO=∠EDB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ODB+∠EDB=90°,即∠ODE=90°,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)∵∠BDE=∠A,
∴∠ABD=∠EBD,而BD⊥AC,
∴△ABC为等腰三角形,
∴AD=CD=![]() AC=8,
AC=8,
在Rt△ABD中,∵tanA=![]() =
=![]() ,
,
∴BD=![]() ×8=6,
×8=6,
∴AB=![]() =10,
=10,
∴⊙O的半径为5.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
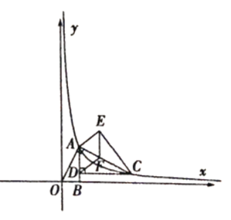
【题目】已知:如图,![]() 的顶点
的顶点![]() 是反比例函数
是反比例函数![]() 图象上一点,过点
图象上一点,过点![]() 作
作![]() 交反比例函数的图象于点
交反比例函数的图象于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]()
(1)求点![]() 的坐标;
的坐标;
(2)将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,连接
,连接![]() ,判断四边形
,判断四边形![]() 的形状并说明理由.
的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,BC=9, CA=12,∠ABC的平分线BD交AC与点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连结EF,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
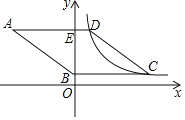
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
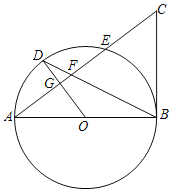
【题目】如图所示,AB是⊙O的直径,G为弦AE的中点,OG的延长线交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为10,tanA=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为![]() 的直径,点C和点G是
的直径,点C和点G是![]() 上的两点,过点C作BG的垂线交BG的延长线于点D延长DC交A的延长线于点E,连接BC,交OD于点F,BC平分∠ABD.
上的两点,过点C作BG的垂线交BG的延长线于点D延长DC交A的延长线于点E,连接BC,交OD于点F,BC平分∠ABD.
(1)求证:CD是![]() 的切线;
的切线;
(2)若![]() ,探索线段OF与FD的数量关系;
,探索线段OF与FD的数量关系;
(3)连接AD,若![]() ,
,![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11月21日,“中国流动科技馆”榆林市第二轮巡展启动仪式在榆阳区青少年校外活动中心盛大举行,此次巡展以“体验科学”为主题.榆林市某中学举行了“科普知识”竞赛,为了解此次“科普知识”竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示.请根据图表信息解答以下问题.
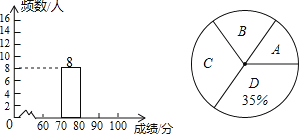

(1)表中a= ;一共抽取了 个参赛学生的成绩;
(2)补全频数分布直方图;
(3)计算扇形统计图中“B”与“C”对应的圆心角度数;
(4)若成绩在80分以上(包括80分)的为“优”等,所抽取学生成绩为“优”的占所抽取学生的百分比是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com