
【题目】甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推岀优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠:乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓按售价付款,优惠期间,设游客的草莓采摘量为x(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙元,y甲、y乙与x之间的函数关系如图所示.
(1)求y甲、y乙与x的函数表达式;
(2)在春节期间,李华一家三口准备去草莓园采摘草莓,采摘的草莓合在一起支付费用,则李华一家应选择哪家草莓园更划算?
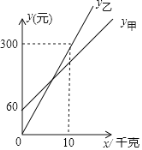
【答案】(1)y甲=18x+60,y乙=30x(2)当采摘量小于5千克且大于0千克时,到家乙莓采摘园更划算
【解析】
(1)根据函数图象和图象中的数据可以解答本题;
(2)根据(1)的结论列不等式或方程解答即可.
解:(1)300÷10=30(元/千克)
根据题意得y甲=18x+60,
设y乙=k2x,根据题意得,
10k2=300,解答k2=30,
∴y乙=30x;
(2)当y甲<y乙,即18x+60<30x,解得x>5,
所以当采摘量大于5千克时,到家草莓采摘园更划算;
当y甲=y乙,即18x+60=30x,解得x=5,
所以当采摘量为5千克时,到两家草莓采摘园所需总费用一样;
当y甲>y乙,即、18x+60>30x,解得x<5,
所以当采摘量小于5千克时,到家乙莓采摘园更划算.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,BC=9, CA=12,∠ABC的平分线BD交AC与点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连结EF,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为![]() 的直径,点C和点G是
的直径,点C和点G是![]() 上的两点,过点C作BG的垂线交BG的延长线于点D延长DC交A的延长线于点E,连接BC,交OD于点F,BC平分∠ABD.
上的两点,过点C作BG的垂线交BG的延长线于点D延长DC交A的延长线于点E,连接BC,交OD于点F,BC平分∠ABD.
(1)求证:CD是![]() 的切线;
的切线;
(2)若![]() ,探索线段OF与FD的数量关系;
,探索线段OF与FD的数量关系;
(3)连接AD,若![]() ,
,![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: ① abc<0;② 2a+b=0; ③ b2-4ac<0;④ 9a+3b+c>0; ⑤ c+8a<0.正确的结论有( ).
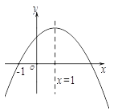
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为4,以BC为直径的半圆O交AB于点D,交AC于点E,则图中阴影部分的面积是( )
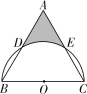
A.2![]() -
-![]() B.2
B.2![]() -
-![]()
C.4![]() +-
+-![]() D.4
D.4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
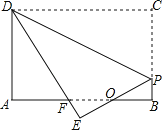
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11月21日,“中国流动科技馆”榆林市第二轮巡展启动仪式在榆阳区青少年校外活动中心盛大举行,此次巡展以“体验科学”为主题.榆林市某中学举行了“科普知识”竞赛,为了解此次“科普知识”竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示.请根据图表信息解答以下问题.
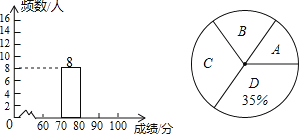

(1)表中a= ;一共抽取了 个参赛学生的成绩;
(2)补全频数分布直方图;
(3)计算扇形统计图中“B”与“C”对应的圆心角度数;
(4)若成绩在80分以上(包括80分)的为“优”等,所抽取学生成绩为“优”的占所抽取学生的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=( )

A.1.2 里B.1.5 里C.1.05 里D.1.02 里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,∠BAC=60°,D为BC边上一点,(不与点B、C)重合,将线段AD绕点A逆时针旋转60°得到AE,连接EC,则∠ACE的度数是__________,线段AC,CD,CE之间的数量关系是_______________.
(2)2,在△ABC中,AB=AC,∠BAC=90°,D为BC边上一点(不与点B、C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,请写出∠ACE的度数及线段AD,BD,CD之间的数量关系,并说明理由.
(3)如图3,在Rt△DBC中,DB=3,DC=5,∠BDC=90°,若点A满足AB=AC,∠BAC=90°,请直接写出线段AD的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com